题目内容
圆Q的半径是5,圆心Q与点P (-2,6 ) 关于直线l:3x-4y+5=0 对称,求圆的标准方程.
考点:关于点、直线对称的圆的方程
专题:直线与圆
分析:设出对称的点的坐标(a,b),利用点P与对称的点的连线与对称轴垂直,以及点P与对称的点的连线的中点在对称轴上,解出对称点的坐标.然后求出圆的方程即可.
解答:
解:设点P (-2,6 )关于直线l:3x-4y+5=0 对称的点的坐标(a,b),
则
×
=-1,且3×
-4×
+5=0,
解得a=4且b=-2,圆Q的圆心(4,-2),半径是5,
圆的标准方程:(x-4)2+(y+2)2=25.
则
| b-6 |
| a+2 |
| 3 |
| 4 |
| a-2 |
| 2 |
| b+6 |
| 2 |
解得a=4且b=-2,圆Q的圆心(4,-2),半径是5,
圆的标准方程:(x-4)2+(y+2)2=25.
点评:本题考查求一个点关于某一条直线的对称点的坐标的求法,利用垂直及中点在轴上两个条件解出对称点的坐标.

练习册系列答案
相关题目
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )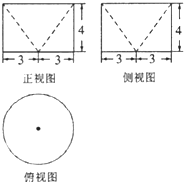

| A、33πcm2 |
| B、42πcm2 |
| C、48πcm2 |
| D、52πcm2 |
已知偶函数f(x)在[0,+∞)上单调递减,则f(1)和f(-10)的大小关系为( )
| A、f(1)>f(-10) |
| B、f(1)<f(-10) |
| C、f(1)=f(-10) |
| D、f(1)与f(-10)的大小关系不确定 |
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2
,则k的取值范围是( )
| 3 |
A、[-
| ||||||||
B、[-∞,-
| ||||||||
C、[-
| ||||||||
D、[-
|
已知a>0,b>0,4a+b=1,则ab的最大值是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
计算定积分
xdx的值( )
| ∫ | 1 -1 |
| A、3 | B、2 | C、1 | D、0 |
 半径为1的半圆中,作如图所示的等腰梯形ABCD,设梯形的上底BC=2x,梯形ABCD的周长为y.
半径为1的半圆中,作如图所示的等腰梯形ABCD,设梯形的上底BC=2x,梯形ABCD的周长为y.