题目内容
已知P是曲线y=
上的一个动点，过点P作圆（x-3）2+y2=1 的切线，切点分别为M，N，当|MN|的值最小时点P的坐标为 ．
| 2x |
考点：圆与圆锥曲线的综合
专题：综合题,圆锥曲线的定义、性质与方程
分析：根据题意，利用等面积可得|MN|=2|ME|=
=2
，所以当|PO1|最小时，|MN|取最小值，故可求．
| 2|PM||O1M| |
| |PO1| |
1-
|
解答：
解：设圆心为O1（3，0），PO1与MN交于E，则|PO1|2=|PM|2+1，
由等面积可知：|MN|=2|ME|=
=2
∴当|PO1|最小时，|MN|取最小值，|PO1|=
=
∴当x=2时，|PO1|有最小值
，
∴点P的坐标为（2，2）．
故答案为：（2，2）．
解：设圆心为O1（3，0），PO1与MN交于E，则|PO1|2=|PM|2+1，由等面积可知：|MN|=2|ME|=
| 2|PM||O1M| |
| |PO1| |
1-
|
∴当|PO1|最小时，|MN|取最小值，|PO1|=
| (x-3)2+y2 |
| (x-2)2+5 |
∴当x=2时，|PO1|有最小值
| 5 |
∴点P的坐标为（2，2）．
故答案为：（2，2）．
点评：本题重点考查圆与抛物线的综合，考查距离最小值的求解，解题的关键是利用等面积可得|MN|=2|ME|=
=2
．
| 2|PM||O1M| |
| |PO1| |
1-
|
练习册系列答案
阳光课堂同步练习系列答案
相关题目
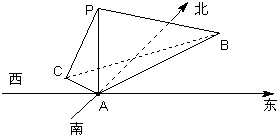在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午9时测得一轮船在海岛北偏东30°，俯角为30°的B处，匀速直行10分钟后，测得该船位于海岛北偏西60°，俯角为45°的C处．从C处开始，该船航向改为正南方向，且速度大小不变，则该船经过10分钟后离开A点的距离为（ ）| A、1千米 | ||
| B、2千米 | ||
C、
| ||
D、2
|
已知函数f（x）=x3+2x+sinx（x∈R），f（x1）+f（x2）＞0，则下列不等式正确的是（ ）
| A、x1＞x2 |
| B、x1＜x2 |
| C、x1+x2＜0 |
| D、x1+x2＞0 |