题目内容
已知a＞0，b＞0，4a+b=1，则ab的最大值是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点：基本不等式
专题：不等式的解法及应用
分析：本题可以直接利用基本不等式求出ab的最大值，得到本题结论．
解答：
解：∵a＞0，b＞0，4a+b=1，
∴4a+b≥2
，
∴4
≤1，
∴ab≤
．
（当且仅当a=
，b=
时，ab取最大值．）
故选C．
∴4a+b≥2
| 4a•b |
∴4
| ab |
∴ab≤
| 1 |
| 16 |
（当且仅当a=
| 1 |
| 8 |
| 1 |
| 2 |
故选C．
点评：本题考查了基本不等式求最值，本题难度不大，属于基础题．
练习册系列答案
相关题目
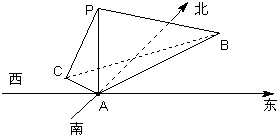在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午9时测得一轮船在海岛北偏东30°，俯角为30°的B处，匀速直行10分钟后，测得该船位于海岛北偏西60°，俯角为45°的C处．从C处开始，该船航向改为正南方向，且速度大小不变，则该船经过10分钟后离开A点的距离为（ ）| A、1千米 | ||
| B、2千米 | ||
C、
| ||
D、2
|
已知函数f（x）=x3+2x+sinx（x∈R），f（x1）+f（x2）＞0，则下列不等式正确的是（ ）
| A、x1＞x2 |
| B、x1＜x2 |
| C、x1+x2＜0 |
| D、x1+x2＞0 |
函数f（x）=2x-3x的零点所在的一个区间是（ ）
| A、（-2，-1） |
| B、（-1，0） |
| C、（1，2） |
| D、（0，1） |
已知f（x）=x2+x，则数列{
}（n∈N*）的前n项和为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数y=f（x）的图象在点（1，f（1））处的切线方程为y=3x-2，则函数g（x）=x2+f（x）的图象在点（1，g（1））处的切线方程为（ ）
| A、5x-y-3=0 |
| B、5x-y+3=0 |
| C、x-5y+3=0 |
| D、x-5y-3=0 |