题目内容
已知点P（-2，6），F2为椭圆
+
=1的右焦点，点M在椭圆上，求|MP|+|MF2|最大值和最小值．
| x2 |
| 25 |
| y2 |
| 16 |
考点：椭圆的简单性质
专题：计算题,作图题,圆锥曲线的定义、性质与方程
分析：由题意作图，从而得F1（-3，0），F2（3，0）；从而由几何意义求最值．
解答：
解：由题意作图如右图，
F1（-3，0），F2（3，0）；
当M在点M″时，|MP|+|MF2|有最小值，
即
=
；
又由|MP|+|MF2|=|MP|+10-|MF1|
=10+|MP|-|MF1|知，
当M在点M′时，|MP|+|MF2|有最大值，
其中|MP|-|MF1|=
=
；
故最大值为10+
．
解：由题意作图如右图，F1（-3，0），F2（3，0）；
当M在点M″时，|MP|+|MF2|有最小值，
即
| (3+2)2+62 |
| 61 |
又由|MP|+|MF2|=|MP|+10-|MF1|
=10+|MP|-|MF1|知，
当M在点M′时，|MP|+|MF2|有最大值，
其中|MP|-|MF1|=
| (-2+3)2+62 |
| 37 |
故最大值为10+
| 37 |
点评：本题考查了圆锥曲线的定义及几何意义的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
复数z满足（z+i）i=-3+i，i为虚数单位，则z等于（ ）
| A、1+2i | B、1-2i |
| C、-1+2i | D、-1-2i |
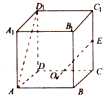如图，在棱长为2的正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，E为CC1的中点，那么异面直线OE与AD1所成角的余弦值等于