题目内容
两圆x2+y2+4y=0,x2+y2+2(a-1)x+2y+a2=0在交点处的切线方程互相垂直,那么实数a的值为 .
考点:圆的切线方程
专题:直线与圆
分析:由题意结合圆的切线性质可得O1A⊥AO2,由勾股定理可得m的值,再用勾股定理求得AB的长度.
解答:
解:根据x2+y2+4y=0,得
x2+(y+2)2=4,
x2+y2+4y=0,①,
x2+y2+2(a-1)x+2y+a2=0,②
①-②,得公共弦的方程为:
2(a-1)x-2y+a2=0,
设交点为(m,n),
∴m2+n2+4n=0 ③
2(a-1)m-2n+a2=0 ④,
•
=-1 ⑤,
联立③④⑤,得
a=±2.
故答案为:±2.
x2+(y+2)2=4,
x2+y2+4y=0,①,
x2+y2+2(a-1)x+2y+a2=0,②
①-②,得公共弦的方程为:
2(a-1)x-2y+a2=0,
设交点为(m,n),
∴m2+n2+4n=0 ③
2(a-1)m-2n+a2=0 ④,
| n+2 |
| m |
| n+1 |
| m-(1-a) |
联立③④⑤,得
a=±2.
故答案为:±2.
点评:本小题考查圆的标准方程、两直线的位置关系等知识,圆的切线性质,属于基础题.

练习册系列答案
相关题目
已知命题p:“?x∈R,总有x2-x+1>0”的否定是“?x∈R,使得x2-x+1≤0”;命题q:在△ABC中,“A>
”是“sinA>
”的必要不充分条件.则有( )
| π |
| 4 |
| ||
| 2 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
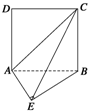 如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )