题目内容
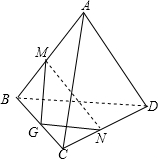
空间四边形ABCD中,对角线AC=10,BD=6,M、N分别是AB、CD的中点,且MN=7,则异面直线AC与BD所成的角为 .
考点:异面直线及其所成的角
专题:空间角
分析:首先通过平行线把异面直线转化为共面直线,利用解三角形知识中的余弦定理求出异面直线的夹角.
解答:
解:取BC的中点G,连接GM,GN
M、N分别是AB、CD的中点,对角线AC=10,BD=6,
所以:GM=
AC=5,GN=
BD=3
在△GMN中,EF=7,GM=5,GN=3
利用余弦定理得:cos∠MGN=|
|=
即:cos∠MGN=
所以:∠MGN=60°
故答案为:60°
所以:异面直线AC与BD所成的角为60°
M、N分别是AB、CD的中点,对角线AC=10,BD=6,
所以:GM=
| 1 |
| 2 |
| 1 |
| 2 |
在△GMN中,EF=7,GM=5,GN=3
利用余弦定理得:cos∠MGN=|
| GM2+GN2-EF2 |
| 2GM•GN |
| 1 |
| 2 |
即:cos∠MGN=
| 1 |
| 2 |
所以:∠MGN=60°
故答案为:60°
所以:异面直线AC与BD所成的角为60°

点评:本题考查的知识要点:异面直线所成的角的应用,余弦定理的应用,属于基础题型.

练习册系列答案
相关题目
已知集合M={-1,0,1},N={-1,0},则M∩N=( )
| A、{-1,0,1} |
| B、{-1,0} |
| C、{-1,1} |
| D、{1,0} |
设函数f(x)=2sin(2x+
)(x∈[-
,
]),在区间D上单调递增,则区间D可以是( )
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
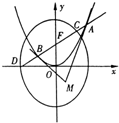 已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点.
已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点.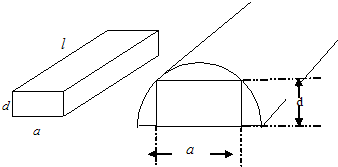 一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.
一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.