题目内容
已知P是以F1、F2为焦点的椭圆
+
=1（a＞b＞0）上一点，若
•
=0，tan∠PF1F2=2，求该椭圆的离心率．
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
考点：椭圆的简单性质
专题：计算题,解三角形,圆锥曲线的定义、性质与方程
分析：设|PF1|=m，根据△PF1F2为直角三角形和tan∠PF1F2=2，可分别表示出|PF2|和|F1F2|，运用椭圆的定义进而表示出a和c，最后根据e=
，求得答案．
| c |
| a |
解答：
解：由题意得△PF1F2为直角三角形，
设|PF1|=m，
由于tan∠PF1F2=
=2，
∴|PF2|=2m，
又由勾股定理得，|F1F2|=
m，
∴椭圆的离心率e=
=
=
=
．
设|PF1|=m，
由于tan∠PF1F2=
| |PF2| |
| |PF1| |
∴|PF2|=2m，
又由勾股定理得，|F1F2|=
| 5 |
∴椭圆的离心率e=
| c |
| a |
| 2c |
| 2a |
| ||
| m+2m |
| ||
| 3 |
点评：本题考查椭圆的定义和性质，考查离心率的求法，考查运算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知a，b∈R，则“a＞b”是“
＞
”成立的（ ）
| a+b |
| 2 |
| ab |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
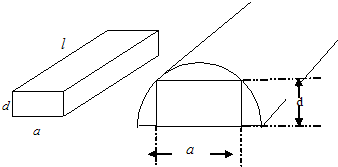一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．