题目内容
已知A点是⊙O的直径CB延长线上的点,过A作⊙O的切线AT,T为切点,∠ATB=30°,若⊙O的半径为4,则AC= .
考点:与圆有关的比例线段
专题:立体几何
分析:连结OT,CT,则OT⊥AT,由已知条件推导出∠OTB=∠TBO=60°,∠TAB=30°,AB=TB=OB=4,由此能求出AC.
解答:
解:如图,A点是⊙O的直径CB延长线上的点,
过A作⊙O的切线AT,T为切点,
连结OT,CT,则OT⊥AT,
∵∠ATB=30°,⊙O的半径为4,
∴∠OTB=∠TBO=60°,∴∠TAB=30°,
∴AB=TB=OB=4,∴AC=4×3=12.
故答案为:12.

过A作⊙O的切线AT,T为切点,
连结OT,CT,则OT⊥AT,
∵∠ATB=30°,⊙O的半径为4,
∴∠OTB=∠TBO=60°,∴∠TAB=30°,
∴AB=TB=OB=4,∴AC=4×3=12.
故答案为:12.
点评:本题考查线段长的求法,是中档题,解题时要认真审题,注意圆的性质的灵活运用.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则tanθ=( )
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
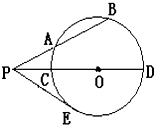 如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7
如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7