题目内容
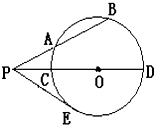如图，⊙O的割线PAB交⊙O于A、B两点，割线PCD经过圆心O，PE是⊙O的切线．已知PA=6，AB=7| 1 |
| 3 |
考点：与圆有关的比例线段
专题：立体几何
分析：由切割线定理得PE2=PC×PD=PA×PB，由此能求出结果．
解答：
解：∵⊙O的割线PAB交⊙O于A、B两点，割线PCD经过圆心O，PE是⊙O的切线，
∴PE2=PC×PD=PA×PB，
∵PA=6，AB=7
，PO=12，
∴PE2=6×(6+7
)=80，解得PE=4
．
设⊙O的半径为r，则（12-r）（12+r）=80，
解得r=8．
∴PE的长为4
，⊙O的半径为8．
∴PE2=PC×PD=PA×PB，
∵PA=6，AB=7
| 1 |
| 3 |
∴PE2=6×(6+7
| 1 |
| 3 |
| 5 |
设⊙O的半径为r，则（12-r）（12+r）=80，
解得r=8．
∴PE的长为4
| 5 |
点评：本题考查与圆有关的线段和圆的半径的求法，是中档题，解题时要认真审题，注意切割线定理的灵活运用．
练习册系列答案
全能测控期末小状元系列答案
相关题目