Question

在区间[1，5]和[2，4]分别取一个数，记为a，b，则方程

x2

a2

+

y2

b2

=1表示焦点在x轴上且离心率小于

3

2

的椭圆的概率为

 

．

Answer 1

考点：几何概型

专题：概率与统计

分析：表示焦点在x轴上且离心率小于

3

2

的椭圆时，（a，b）点对应的平面图形的面积大小和区间[1，5]和[2，4]分别各取一个数（a，b）点对应的平面图形的面积大小，并将他们一起代入几何概型计算公式进行求解．

解答： 解：∵方程

x2

a2

+

y2

b2

=1表示焦点在x轴上且离心率小于

3

2

的椭圆，
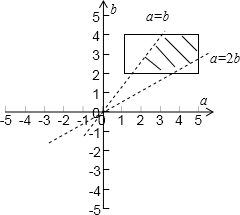
∴a＞b＞0，a＜2b，
它对应的平面区域如图中阴影部分所示：
则方程

x2

a2

+

y2

b2

=1表示焦点在x轴上且离心率小于

3

2

的概率为
P=

S阴影

S矩形

=1-

1 2 ×1× 1 2 + 1 2 ×(1+3)×2

2×4

=

15

32

，
故答案为：

15

32

点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．