题目内容
已知双曲线C:x2-
=1,过点P(-1,-2)的直线交C于A,B两点,且点P为线段AB的中点.
(1)求直线AB的方程;
(2)求弦长|AB|的值.
| y2 |
| 2 |
(1)求直线AB的方程;
(2)求弦长|AB|的值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)可先设A(x1,y1),B(x2,y2),再分别代入双曲线方程,作差即可求出直线斜率,进而可求直线方程.
(2)把(1)中所求直线方程代入双曲线方程,利用根与系数关系,求x1,x2,再利用弦长公式求线段AB的长.
(2)把(1)中所求直线方程代入双曲线方程,利用根与系数关系,求x1,x2,再利用弦长公式求线段AB的长.
解答:
解(1)设A(x1,y1),B(x2,y2),则x1+x2=-2,y1+y2=-4,
由x12-
=1,x22-
=1作差得(x1+x2)(x1-x2)-
(y1+y2)(y1-y2)=0,
∴kAB=
=1,
∴直线AB方程为y=x-1.
(2)把y=x-1代入x2-
=1,消去y得x2+2x-3=0
∴x1=1,x2=-3,从而得|AB|=
•|x1-x2|=4
.
由x12-
| y12 |
| 2 |
| y22 |
| 2 |
| 1 |
| 2 |
∴kAB=
| y1-y2 |
| x1-x2 |
∴直线AB方程为y=x-1.
(2)把y=x-1代入x2-
| y2 |
| 2 |
∴x1=1,x2=-3,从而得|AB|=
| 1+1 |
| 2 |
点评:本题考查点差法求中点弦方程以及弦长公式求弦长,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知正方形ABCD,AB=2,AC、BD交点为O,在ABCD内随机取一点E,则点E满足OE<1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知不同的直线l,m,不同的平面α,β,下命题中:
①若α∥β,l?α,则l∥β
②若α∥β,l⊥α,则l⊥β
③若l∥α,m?α,则l∥m
④若α⊥β,α∩β=l,m⊥l
则真命题的个数有( )
①若α∥β,l?α,则l∥β
②若α∥β,l⊥α,则l⊥β
③若l∥α,m?α,则l∥m
④若α⊥β,α∩β=l,m⊥l
则真命题的个数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
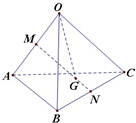 已知空间四边形OABC,其对角线为OB,AC,M,N分别是边OA,BC的中点,点G在线段MN上,若MG=λGN,且
已知空间四边形OABC,其对角线为OB,AC,M,N分别是边OA,BC的中点,点G在线段MN上,若MG=λGN,且