题目内容
有6个房间安排4个旅游者住宿,每人可以随意进哪一间,而且一个房间也可以住多个人,求下列问题中各有多少种不同的住法?
(1)每人随意选择,则所有的入住方法;
(2)第1号房间有1人,第2号房间有3人;
(3)指定的4个房间中各有1人;
(4)恰有1个房间中有2人;
(5)恰有2个房间中各有2人.
(1)每人随意选择,则所有的入住方法;
(2)第1号房间有1人,第2号房间有3人;
(3)指定的4个房间中各有1人;
(4)恰有1个房间中有2人;
(5)恰有2个房间中各有2人.
考点:计数原理的应用
专题:排列组合
分析:根据排列组合的原则,先选再排,看看是分类还是分步,分别按(1),(2),(3),(4),(5)的要求进行排列即可.
解答:
解:4个人住进6个房间,所有可能的住房结果总数为:
(1)根据分步计数原理,4个旅游者每一人算一步,每一步都有6种选择,共有64种;
(2)先安排第一房间,再安排地三个房间,则第一号房间1人,第二号房间3人的不同住法总数为:
=4(种)
(3)指定的4个房间每间1人,就是4人住进4个房间的排列,共有
=24种不同住法;
(4)恰有一个房间中有两人,先选2人,再选一个房间,住进这一个房间,剩下的任意排,共有
=720种;
(5)恰有2个房间中各有2人
=60种.
(1)根据分步计数原理,4个旅游者每一人算一步,每一步都有6种选择,共有64种;
(2)先安排第一房间,再安排地三个房间,则第一号房间1人,第二号房间3人的不同住法总数为:
| C | 1 4 |
| •C | 3 3 |
(3)指定的4个房间每间1人,就是4人住进4个房间的排列,共有
| A | 4 4 |
(4)恰有一个房间中有两人,先选2人,再选一个房间,住进这一个房间,剩下的任意排,共有
| C | 2 4 |
| •C | 1 6 |
| •A | 3 5 |
(5)恰有2个房间中各有2人
| ||
|
| •A | 2 5 |
点评:本题考查了排列组合中先选再排的问题,关键读懂题意,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
命题p:a(a-1)≤0;命题q:y=xa(x为自变量)在第一象限是增函数,p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知数列{an}为等差数列,且a3+a9=
,sina6cosa6的值为( )
| 4π |
| 3 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、-
|
设a>b>0,a+b=1且x=(
)b,y=log (
+
)a,z=log
a,则x,y,z的大小关系是( )
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
| A、y<x<z |
| B、z<y<x |
| C、y<z<x |
| D、x<y<z |
设全集U={x∈N|x≤5},A={0,1,2,3},B={0,3,4,5},则B∩(∁UA)=( )
| A、{3} |
| B、{4,5} |
| C、{3,4,5} |
| D、{4,5,6} |
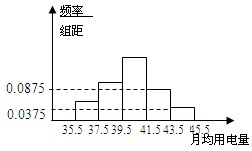 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3.