题目内容
设a＞b＞0，a+b=1且x=（
）b，y=log (
+
)a，z=log
a，则x，y，z的大小关系是（ ）
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
| A、y＜x＜z |
| B、z＜y＜x |
| C、y＜z＜x |
| D、x＜y＜z |
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用对数函数和指数函数的单调性即可得出．
解答：
解：∵a＞b＞0，a+b=1，∴
+
＞
＞1，
∴y=log (
+
)a＜z=log
a，即y＜z．
∵a＞b＞0，a+b=1，
∴
＞1，
＞1，0＜b＜a＜1．
∴z=log
a＜log
1=0，x=(
)b＞(
)0=1．
∴x＞z．
∴y＜z＜x．
故选：C．
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
∴y=log (
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
∵a＞b＞0，a+b=1，
∴
| 1 |
| b |
| 1 |
| a |
∴z=log
| 1 |
| b |
| 1 |
| b |
| 1 |
| a |
| 1 |
| a |
∴x＞z．
∴y＜z＜x．
故选：C．
点评：本题考查了对数函数和指数函数的单调性，属于难题．
练习册系列答案
优等生题库系列答案
相关题目
已知an=3n+2，n∈N*，如果执行如图所示的程序框图，那么输出的S等于（ ）
| A、18.5 | B、37 |
| C、185 | D、370 |
已知点P（x，y）的坐标满足条件
，O是坐标原点，则|OP|的最小值为（ ）
|
A、
| ||||
B、
| ||||
| C、5 | ||||
D、2
|
已知全集U=R，集合A={x||x-2|＜1}，B={x|y=
}，则A∩B=（ ）
| 4-2x |
| A、（1，2） |
| B、（2，3） |
| C、[2，3） |
| D、（1，2] |
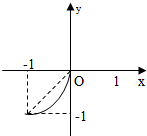已知定义在（-1，0）上的函数y=f（x）的图象如图所示，对于满足-1＜x1＜x2＜0的任意x1，x2，错误的结论是（ ）| A、当x∈（-1，0）时，x＞f（x） |
| B、当x∈（-1，0）时，导函数f′（x）为增函数 |
| C、f（x2）-f（x1）≤x2-x1 |
| D、x1f（x2）＞x2f（x1） |
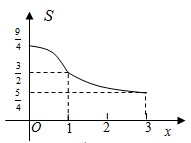
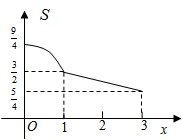
如图在展览厅有一展台，展台是边长为1米的正方体ABCD-A1B1C1D1，面AA1D1D紧靠墙面，一移动光源P在竖直旗杆MN上移动，其中点N在地面上且点N在面BB1C1C上的投影恰好是BC的中点R，MN=3米，NR=2米，设NP=x米，在光源P的照射下，正方体ABCD-A1B1C1D1在面A1B1C1D1紧靠墙面的投影（包括面AA1D1D）的面积为S（x）平方米，则函数y=S（x）的大致图象是（ ）
