题目内容
已知数列{an}为等差数列，且a3+a9=
，sina6cosa6的值为（ ）
| 4π |
| 3 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、-
|
考点：等差数列的性质
专题：等差数列与等比数列
分析：利用等差数列的性质a3+a9=2a6，及a3+a9=
，可求得a6=
，从而可求sina6cosa6的值．
| 4π |
| 3 |
| 2π |
| 3 |
解答：
解：∵数列{an}为等差数列，且a3+a9=2a6=
，
∴a6=
，
∴sina6cosa6=sin
•cos
=
×（-
）=-
，
故选：A．
| 4π |
| 3 |
∴a6=
| 2π |
| 3 |
∴sina6cosa6=sin
| 2π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
故选：A．
点评：本题考查等差数列的性质，求得a6=
是关键，属于中档题．
| 2π |
| 3 |
练习册系列答案
相关题目
已知i是虚数单位，复数z的共轭复数是
，如果|z|+
=8-4i，那么z等于（ ）
. |
| z |
. |
| z |
| A、-3-4i | B、-3+4i |
| C、4+3i | D、3+4i |
已知点P（x，y）的坐标满足条件
，O是坐标原点，则|OP|的最小值为（ ）
|
A、
| ||||
B、
| ||||
| C、5 | ||||
D、2
|
复数z为纯虚数，若（2-i）z=a+i（i为虚数单位），则实数a的值为（ ）
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
已知全集U=R，集合A={x||x-2|＜1}，B={x|y=
}，则A∩B=（ ）
| 4-2x |
| A、（1，2） |
| B、（2，3） |
| C、[2，3） |
| D、（1，2] |
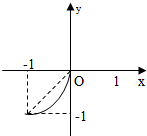已知定义在（-1，0）上的函数y=f（x）的图象如图所示，对于满足-1＜x1＜x2＜0的任意x1，x2，错误的结论是（ ）| A、当x∈（-1，0）时，x＞f（x） |
| B、当x∈（-1，0）时，导函数f′（x）为增函数 |
| C、f（x2）-f（x1）≤x2-x1 |
| D、x1f（x2）＞x2f（x1） |