题目内容
已知等差数列{an}中,公差d≠0,a1=2,且a1,a3,a7成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=
,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=
| 1 |
| an•an+1 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由题意列出方程,解得公差d,写出通项公式;
(Ⅱ)利用裂项相消法对数列求和即得结论.
(Ⅱ)利用裂项相消法对数列求和即得结论.
解答:
解:(I)设数列{an}的公差为d
∵a1,a3,a7成等比数列
∴
=a1a7,∴(a1+2d)2=a1(a1+6d)
又a1=2,∴d=1或d=0(舍去)
∴an=2+(n-1)•1=n+1;
(Ⅱ)由(Ⅰ)得bn=
=
-
,
∴Tn=b1+b2+…+bn=
-
+
-
+…+
-
=
-
=
.
∵a1,a3,a7成等比数列
∴
| a | 2 3 |
又a1=2,∴d=1或d=0(舍去)
∴an=2+(n-1)•1=n+1;
(Ⅱ)由(Ⅰ)得bn=
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴Tn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+2) |
点评:本题考查等差数列的性质及裂项相消法对数列求和,注意方程思想在解题中的运用,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知i是虚数单位,复数z的共轭复数是
,如果|z|+
=8-4i,那么z等于( )
. |
| z |
. |
| z |
| A、-3-4i | B、-3+4i |
| C、4+3i | D、3+4i |
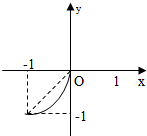 已知定义在(-1,0)上的函数y=f(x)的图象如图所示,对于满足-1<x1<x2<0的任意x1,x2,错误的结论是( )
已知定义在(-1,0)上的函数y=f(x)的图象如图所示,对于满足-1<x1<x2<0的任意x1,x2,错误的结论是( )| A、当x∈(-1,0)时,x>f(x) |
| B、当x∈(-1,0)时,导函数f′(x)为增函数 |
| C、f(x2)-f(x1)≤x2-x1 |
| D、x1f(x2)>x2f(x1) |