题目内容
若（1-ax）5展开式中各项系数和为32，其中a∈R，该展开式中含x2项的系数为 ．
考点：二项式系数的性质
专题：二项式定理
分析：根据展开式中各项系数和为32求得a=-1，再利用通项公式求得展开式中含x2项的系数．
解答：
解：在（1-ax）5展开式中，令x=1，可得各项系数和为（1-a）5 =32，
∴a=-1，故（1-ax）5 =（1+x）5展开式中含x2项的系数为
=10，
故答案为：10．
∴a=-1，故（1-ax）5 =（1+x）5展开式中含x2项的系数为
| C | 2 5 |
故答案为：10．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
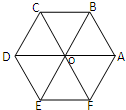（1）如图，正六边形ABCDEF中，点O为其中心，以这七个点为起点与终点的向量中，与向量
已知函数y=Asin（ωx+φ）（A＞0，ω＞0，0≤φ＜π）的部分图象如图所示，则A=