题目内容
函数y=
-sinx 的单调递减区间是 ．
| x |
| 2 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，令导函数小于0，解出即可．
解答：
解：∵y′=
-cosx，
令y′＜0，即cosx＞
，
解得：-
+2kπ＜x＜
+2kπ，
故答案为：（-
+2kπ，
+2kπ）．
| 1 |
| 2 |
令y′＜0，即cosx＞
| 1 |
| 2 |
解得：-
| π |
| 3 |
| π |
| 3 |
故答案为：（-
| π |
| 3 |
| π |
| 3 |
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
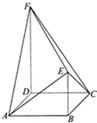如图，多面体ABCDEF中，面ABCD为边长为a的菱形，且∠DAB=60°，DF=2BE=2a，DF∥BE，DF⊥平面ABCD
如图所示，过抛物线y=