题目内容
已知函数f（x）的导函数为f′（x），且f（x）=2xf′（1）+lnx，则f′（x）= ．
考点：导数的运算
专题：导数的概念及应用
分析：对函数f（x）的解析式求导，得到其导函数，把x=1代入导函数中，列出关于f'（1）的方程，进而得到f'（1）的值，确定出函数f（x）的解析式，问题得以解决．
解答：
解：求导得：f′（x）=2f′（1）+
，
令x=1，得到f′（1）=2f′（1）+1，
解得：f′（1）=-1，
∴f（x）=-2x+lnx，
∴f′（x）=-2+
，
故答案为：-2+
．
| 1 |
| x |
令x=1，得到f′（1）=2f′（1）+1，
解得：f′（1）=-1，
∴f（x）=-2x+lnx，
∴f′（x）=-2+
| 1 |
| x |
故答案为：-2+
| 1 |
| x |
点评：此题考查了导数的运算，以及函数的值．运用求导法则得出函数的导函数，求出常数f'（1）的值，从而确定出函数的解析式是解本题的关键，属于基础题
练习册系列答案
阅读快车系列答案
相关题目
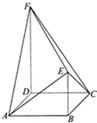如图，多面体ABCDEF中，面ABCD为边长为a的菱形，且∠DAB=60°，DF=2BE=2a，DF∥BE，DF⊥平面ABCD
如图，在正四面体PABC中，若E，F分别在棱PC，AB上，且