题目内容
15.已知集合A={x∈N|-2<x<4},$B=\{x|\frac{1}{2}≤{2^x}≤4\}$,则A∩B=( )| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {1,2} | D. | {0,1,2} |
分析 化简集合A、B,根据交集的定义写出A∩B.
解答 解:集合A={x∈N|-2<x<4}={0,1,2,3},
$B=\{x|\frac{1}{2}≤{2^x}≤4\}$={x|-1≤x≤2},
则A∩B={0,1,2}.
故选:D.
点评 本题考查了集合的化简运算问题,是基础题.

练习册系列答案
相关题目
6.函数f(x)=x2-x-2,x∈[-3,3],那么任取一点x0∈[-3,3],使f(x0)≤0的概率是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{3}$ |
3.已知双曲线${C_1}:\frac{x^2}{2}-{y^2}=1$与双曲线${C_2}:\frac{x^2}{2}-{y^2}=-1$,给出下列说法,其中错误的是( )
| A. | 它们的焦距相等 | B. | 它们的焦点在同一个圆上 | ||
| C. | 它们的渐近线方程相同 | D. | 它们的离心率相等 |
20.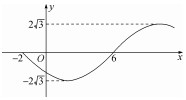 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
5.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )


| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
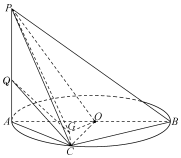 如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.


