Question

已知函数f（x）=

-x，x＜0 x ，x≥0.

使关于x的方程f（x）=a（x+1）有三个不相等的实数根的充分不必要条件是（　　）

• A、{a|a≥

  1

  2

  }
• B、{a|

  1

  2

  ＜a＜1}
• C、{a|0＜a＜

  1

  2

  }
• D、{a|0＜a＜

  1

  4

  }

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：由题意可得，直线y=a（x+1）与曲线y=

x

相交时，与f（x）的图象有三个交点，求出直线与曲线y=

x

相切时的斜率，即可得到a的取值范围．再根据要求的a的范围应是它的子集，可得结论．

解答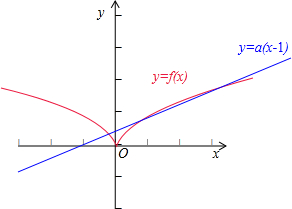： 解：本题即求函数y=f（x）的图象和直线y=a（x+1）的图象有三个不同的交点的充分不必要条件，
下边先求函数y=f（x）的图象和直线y=a（x+1）的图象有三个不同的交点的充要条件．
作出函数f（x）的图象，如右图：作出直线y=a（x+1），则直线恒过（-1，0），
关于x的方程f（x）=a（x+1）有三个不相等的实数根，即为当直线与曲线y=

x

相交时，
与f（x）的图象有三个交点，
当直线与曲线y=

x

相切时，设切点为（m，

m

），
则y′=

1

2

•

1

x

，则切线斜率为

1

2

•

1

m

=a，
又a（m+1）=

m

，由此解得，a=

1

2

（负的舍去），故此时a的取值范围是（0，

1

2

）．
而要求的a的范围应是（0，

1

2

）的子集，结合所给的选项，
故选：D．

点评：本题考查分段函数及运用，考查分段函数的图象和应用，考查数形结合的思想方法，以及运用导数求切线方程，属于中档题．