题目内容
已知函数f（x）=
x3-ax2+b在x=2处有极值．
（1）求a的值；
（2）求函数f（x）的单调区间．
| 1 |
| 3 |
（1）求a的值；
（2）求函数f（x）的单调区间．
考点：利用导数研究函数的极值,利用导数研究函数的单调性
专题：导数的概念及应用
分析：（1）先求导数，令x=2时导数等于零，求出a的值，要验证2两侧导数是否异号；
（2）求导数，解不等式导数大于零得原函数增区间，导数小于零得减区间．
（2）求导数，解不等式导数大于零得原函数增区间，导数小于零得减区间．
解答：
解：（1）由题意得f′（x）=x2-2ax，令f′（2）=0得a=1，经验证a=1时x=2两侧导数异号，所以a=1符合题意．
（2）由（1）知f′（x）=x2-2x，令f′（x）＞0得x＞2或x＜0；令f′（x）＜0得0＜x＜2，
所以原函数的增区间为（-∞，0）和（2，+∞），减区间为（0，2）．
（2）由（1）知f′（x）=x2-2x，令f′（x）＞0得x＞2或x＜0；令f′（x）＜0得0＜x＜2，
所以原函数的增区间为（-∞，0）和（2，+∞），减区间为（0，2）．
点评：对于可导函数的极值点理解必须从两个方面，一是导数为零，二是两侧导数异号；求单调区间就是解导数不等式，注意若同为增区间不止一个，要用逗号隔开．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
已知A={x|y=
}，B={y|y=
}，则∁BA是（ ）
| ||
| |x|-5 |
| x2-6x+13 |
| A、[2，+∞） |
| B、（2，4）∪{5} |
| C、[4，5）∪（5，+∞） |
| D、（2，4） |
方程x2-3x+1=0的两根e1和e2可以分别为（ ）
| A、椭圆与双曲线的离心率 |
| B、两条抛物线的离心率 |
| C、两个椭圆的离心率 |
| D、椭圆与抛物线的离心率 |
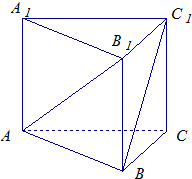在正三棱柱ABC-A1B1C1中，AB1⊥BC1，求BC1与平面ABB1A1所成角的正弦值．（正三棱柱：上下底面为正三角形的直棱柱，底面边长不一定等于侧棱长）