题目内容
已知函数f(x)=-3x2-3x+4b2+
,b>0,x∈[-b,b],且f(x)的最大值为7,求b的值.
| 9 |
| 4 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:首先把二次函数的一般式转化成顶点式,然后对对称轴与补丁区间进行讨论,根据相应的结果进行判断,最后确定b的值.
解答:
解:函数f(x)=-3x2-3x+4b2+
=-3(x+
)2+
+4b2+
∴函数是开口方向向下,对称轴是x=-
的抛物线
①当-b≤-
≤b时,f(x)max=f(-
)=
+4b2+
=7
解得:b=±1(负值舍去)
∴b=1
②当-b>-
时,即b<
,f(x)max=f(-b)=-3b2+3b+4b2+
=7
解得:b=
(负值舍去)
∴b=
>
不符合题意故舍去.
③当b<-
时不符合题意
综上所述:b=1
故答案为:b=1
| 9 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
∴函数是开口方向向下,对称轴是x=-
| 1 |
| 2 |
①当-b≤-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
解得:b=±1(负值舍去)
∴b=1
②当-b>-
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
解得:b=
-12±8
| ||
| 8 |
∴b=
-12+8
| ||
| 8 |
| 1 |
| 2 |
③当b<-
| 1 |
| 2 |
综上所述:b=1
故答案为:b=1
点评:本题考查的知识点:二次函数一般式与顶点式的转换,对称轴和不定区间的讨论及相关的运算问题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
与集合M={x∈R|x2+16=0}相等的集合是( )
| A、{-16,16} |
| B、{-4,4} |
| C、{x∈R|x2+6=0} |
| D、{x∈R|x2=16} |
在△ABC中,其中有两解的是( )
| A、a=8,b=15,A=30° |
| B、a=30,b=25,A=150° |
| C、a=72,b=50,A=135° |
| D、a=18,b=16,A=60° |
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
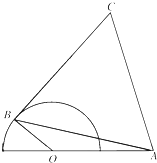 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.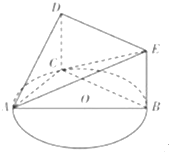 如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=
如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=