题目内容
四边形ABCD是矩形,AB=2,BC=1,PC⊥平面AC,PC=2,则点P到直线BD的距离为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:连结BD,作CE⊥BD,交BD于E,连结PE,则由三垂线定理得PE⊥BD,从而PE就是点P到直线BD的距离.
解答:
解:如图,连结BD,作CE⊥BD,交BD于E,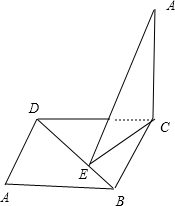
连结PE,则由三垂线定理得PE⊥BD,
∴PE就是点P到直线BD的距离,
∵四边形ABCD是矩形,AB=2,BC=1,PC⊥平面AC,PC=2,
∴BD=
=
,
∵
BD•CE=
BC•DC,
∴CE=
=
=
,
∴PE=
=
=
.
故答案为:
.

连结PE,则由三垂线定理得PE⊥BD,
∴PE就是点P到直线BD的距离,
∵四边形ABCD是矩形,AB=2,BC=1,PC⊥平面AC,PC=2,
∴BD=
| 4+1 |
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| BC•DC |
| BD |
| 1×2 | ||
|
2
| ||
| 5 |
∴PE=
| AC2+EC2 |
4+
|
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题考查点到直线的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
A如图是一个正方体的展开图,则在原正方体中( )


| A、AB∥CD |
| B、AB∥EF |
| C、CD∥GH |
| D、AB∥GH |
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、48-16π |
| B、96-4π |
| C、96-8π |
| D、48-4π |
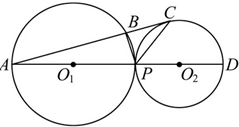 如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证:
如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证: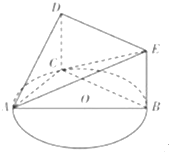 如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=
如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=