题目内容
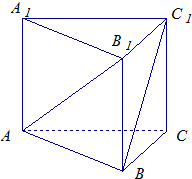 在正三棱柱ABC-A1B1C1中,AB1⊥BC1,求BC1与平面ABB1A1所成角的正弦值.(正三棱柱:上下底面为正三角形的直棱柱,底面边长不一定等于侧棱长)
在正三棱柱ABC-A1B1C1中,AB1⊥BC1,求BC1与平面ABB1A1所成角的正弦值.(正三棱柱:上下底面为正三角形的直棱柱,底面边长不一定等于侧棱长)考点:直线与平面所成的角
专题:计算题,空间角
分析:取A1B1中点D,设A1B1=2a,连接C1D,BD,可得∠C1BD为所求角,进而可求BC1与平面ABB1A1所成角的正弦值.
解答:
解:取A1B1中点D,设A1B1=2a,连接C1D,BD,∴C1D=
a,
设B1B=x,则
∵C1D⊥A1B1,
,∴AB1⊥C1D,∠C1BD为所求角,
∴B1M=
.
∵△ABM~△B1DM,∴
=
=
⇒x=
a,
∴sin∠C1BD=
,即BC1与平面ABB1A1所成角的正弦值为
.
| 3 |
设B1B=x,则
∵C1D⊥A1B1,
|
∴B1M=
| ax | ||
|
∵△ABM~△B1DM,∴
| B1M |
| B1A |
| 1 |
| 3 |
| ||||
|
| 2 |
∴sin∠C1BD=
| ||
| 2 |
| ||
| 2 |
点评:本题考查线面垂直的判定与性质,考查线面角,解题的关键是掌握线面垂直的判定与性质,正确作出线面角.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、48-16π |
| B、96-4π |
| C、96-8π |
| D、48-4π |
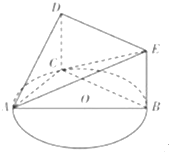 如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=
如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=