题目内容
设函数f(x)=|x+a|,g(x)=x-1,对于?x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是 .
考点:函数恒成立问题
专题:计算题,函数的性质及应用
分析:根据函数f(x)=|x+a|,g(x)=x-1,对于?x∈R,不等式f(x)≥g(x)恒成立,可得-a≤1,即可求出实数a的取值范围.
解答:
解:由题意,函数f(x)=|x+a|,g(x)=x-1,对于?x∈R,不等式f(x)≥g(x)恒成立,
∴-a≤1,
∴a≥-1,
∴实数a的取值范围是a≥-1.
故答案为:a≥-1.
∴-a≤1,
∴a≥-1,
∴实数a的取值范围是a≥-1.
故答案为:a≥-1.
点评:本题考查函数恒成立问题,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
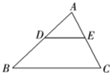 如图,已知D、E分别是△ABC的AB、AC边上一点,DE∥BC,且S△ADE:S四边形DBCE=1:3,那么AD:AB等于( )
如图,已知D、E分别是△ABC的AB、AC边上一点,DE∥BC,且S△ADE:S四边形DBCE=1:3,那么AD:AB等于( )A、1:
| ||
| B、1:2 | ||
| C、1:3 | ||
| D、1:4 |
