题目内容
已知不等式x2+mx>4x+m-4
(1)若对一切实数x使得不等式恒成立,求实数m的取值范围;
(2)若对于0≤m≤4的所有实数m,不等式恒成立,求实数x的取值范围.
(1)若对一切实数x使得不等式恒成立,求实数m的取值范围;
(2)若对于0≤m≤4的所有实数m,不等式恒成立,求实数x的取值范围.
考点:二次函数的性质,函数恒成立问题
专题:函数的性质及应用
分析:(1)中不等式恒成立,需△<0,解出即可,(2)只需转化表达式为不等式恒成立.
解答:
解:(1)∵x2+mx>4x+m-4,
∴x2+mx-4x-m+4>0,
∴△=(m-4)2+4(m-4)<0,
解得:0<m<4.
(2):x2+mx>4x+m-4,可整理为(x-1)m+x2-4x+4>0,
∵对于0≤m≤4的所有实数m,不等式恒成立,
∴有
,
即
,
解得x≠0,且x≠2,
∴实数x的取值范围为:(-∞,0)∪(0,2)∪(2,+∞);
∴x2+mx-4x-m+4>0,
∴△=(m-4)2+4(m-4)<0,
解得:0<m<4.
(2):x2+mx>4x+m-4,可整理为(x-1)m+x2-4x+4>0,
∵对于0≤m≤4的所有实数m,不等式恒成立,
∴有
|
即
|
解得x≠0,且x≠2,
∴实数x的取值范围为:(-∞,0)∪(0,2)∪(2,+∞);
点评:本题考查函数恒成立问题、一元二次不等式的解法,考查转化思想、分类讨论思想,考查学生解决问题的能力.

练习册系列答案
相关题目
已知a=0,7-
,b=0.6-
,c=log2.11.5,则a,b,c的大小关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、c<a<b |
| B、c<b<a |
| C、a<b<c |
| D、b<a<c |
已知函数f(x)=
x2+(a-1)x+3在区间(-∞,4]上单调递减,则a的取值范围( )
| 1 |
| 2 |
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-∞,-3) |
| D、(-∞,-3] |
给定命题p:函数y=ln
为奇函数;命题q:函数y=
为偶函数,下列说法正确的是( )
| 1-x |
| x+1 |
| ex-1 |
| ex+1 |
| A、p∨q是假命题 |
| B、¬p∧q是假命题 |
| C、p∧q是真命题 |
| D、¬p∨q是真命题 |
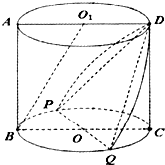 在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.
在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.