题目内容
已知函数f（x）=
x2+（a-1）x+3在区间（-∞，4]上单调递减，则a的取值范围（ ）
| 1 |
| 2 |
| A、[-3，+∞） |
| B、（-3，+∞） |
| C、（-∞，-3） |
| D、（-∞，-3] |
考点：二次函数的性质
专题：函数的性质及应用
分析：利用二次函数的图象与性质得，二次函数f（x）在其对称轴左侧的图象下降，由此得到关于a的不等关系，从而得到实数a的取值范围．
解答：
解：由于二次函数的二次项系数大于0，
∴其对称轴左侧的图象下降，是减函数，
∴1-a≥4，
∴a≤-3．
故选：D．
∴其对称轴左侧的图象下降，是减函数，
∴1-a≥4，
∴a≤-3．
故选：D．
点评：本小题主要考查函数单调性的应用、二次函数的性质、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知2a+b=t（a＞0，b＞0），t为常数，若ab的最大值为2时，a2+b2=（ ）
| A、2 | B、3 | C、4 | D、5 |
某科室派出4名调研员到3个学校，调研高三复习备考近况，要求每个学校至少一名，则不同的分配方案的种数是（ ）
| A、144 | B、72 | C、36 | D、48 |
已知角α的终边经过点P（m，4），且cosα=-
，则m等于（ ）
| 3 |
| 5 |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
“3a＞3b”是“lna＞lnb”的（ ）
| A、充分不必要条件 |
| B、既不充分也不必要条件 |
| C、充要条件 |
| D、必要不充分条件 |
已知等差数列{an}，a2+a18=36，则a5+a6+…+a15=（ ）
| A、130 | B、198 |
| C、180 | D、156 |
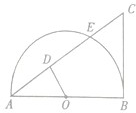如图，过点C作半圆O的切线CB，切点为B，直线AC与半圆O的交点分别为A、E，过圆心O作OD⊥AC垂点为D．