题目内容
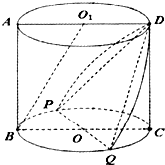 在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.
在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.(Ⅰ)求证:O1B∥平面DPQ;
(Ⅱ)用平面DPQ截圆柱OO1的侧面可得到半个椭圆,该半椭圆所在椭圆以PQ为短轴,OD为长半轴,若PQ=2,且椭圆的离心率为
| ||
| 2 |
考点:直线与平面垂直的判定,旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:(Ⅰ)连结DO,证明O1B∥DO,通过O1B?平面DPQ,DO?平面DPQ,即可证明O1B∥平面DPQ;
(Ⅱ)用平面DPQ截圆柱OO1的侧面可得到半个椭圆,该半椭圆所在椭圆以PQ为短轴,OD为长半轴,若PQ=2,且椭圆的离心率为
,求出圆柱的高,即可求圆柱OO1的体积.
(Ⅱ)用平面DPQ截圆柱OO1的侧面可得到半个椭圆,该半椭圆所在椭圆以PQ为短轴,OD为长半轴,若PQ=2,且椭圆的离心率为
| ||
| 2 |
解答:
解:(Ⅰ)连结DO,由题意可得,
O1D∥BO,且O1D=BO,∴四边形O1BOD为平行四边形,
∴O1B∥DO,
又∵O1B?平面DPQ,
DO?平面DPQ,
∴O1B∥平面DPQ.
(Ⅱ)设椭圆的长半轴为a,短半轴为b,半焦距为c,
∵椭圆的离心率为
.
∴
=
∵a2=b2+c2=b2+
a2,
∴
=
∵a=OD,b=OQ,∴
=
,
∵直径PQ=2∴OC=OQ=1,∴OD=2,
在Rt△DCO中,可求得母线DC=
,
即圆柱OO1的高h=
,
因此,圆柱OO1的体积V=Sh=
π.
O1D∥BO,且O1D=BO,∴四边形O1BOD为平行四边形,
∴O1B∥DO,
又∵O1B?平面DPQ,
DO?平面DPQ,
∴O1B∥平面DPQ.
(Ⅱ)设椭圆的长半轴为a,短半轴为b,半焦距为c,
∵椭圆的离心率为
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
| 3 |
| 4 |
∴
| b |
| a |
| 1 |
| 2 |
∵a=OD,b=OQ,∴
| OQ |
| OD |
| 1 |
| 2 |
∵直径PQ=2∴OC=OQ=1,∴OD=2,
在Rt△DCO中,可求得母线DC=
| 3 |
即圆柱OO1的高h=
| 3 |
因此,圆柱OO1的体积V=Sh=
| 3 |
点评:本题考查直线与直线,直线与平面的位置关系,圆锥曲线的性质,柱体的体积公式的应用,考查空间想象能力以及逻辑推理能力计算能力.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目