题目内容
设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2x.若对任意的x∈[a,a+2],不等式f(x+a)≥f2(x)恒成立,求实数a的取值范围.
考点:奇偶性与单调性的综合
专题:综合题,函数的性质及应用
分析:根据函数为偶函数,求出函数f(x)的表达式,然后将不等式f(x+a)≥f2(x)化简,对a进行讨论,将x解出来,做到参数分离,由恒成立思想,即可求出a的范围.
解答:
解:由题意,f(x)=
(4分)
(1)当a≥0时,即有2x+a≥22x,x≤a,不合 (6分)
(2)当a+2≤0时,即有(
)x+a≥(
)2x,x≥a,恒成立,a≤-2符合 (8分)
(3)当-2<a<0时,若x+a>0,则a+2≥-a,a≥-1由(1)得不合
若x<0由(2)得成立,则x+a<0,x>0时恒成立,即(
)x+a≥22x,x≤-
,
∴a+2≤-
,a≤-
,∴-2<a≤-
(14分)
综上,实数a的取值范围a≤-
(15分)
|
(1)当a≥0时,即有2x+a≥22x,x≤a,不合 (6分)
(2)当a+2≤0时,即有(
| 1 |
| 2 |
| 1 |
| 2 |
(3)当-2<a<0时,若x+a>0,则a+2≥-a,a≥-1由(1)得不合
若x<0由(2)得成立,则x+a<0,x>0时恒成立,即(
| 1 |
| 2 |
| a |
| 3 |
∴a+2≤-
| a |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
综上,实数a的取值范围a≤-
| 3 |
| 2 |
点评:本题主要考查函数的奇偶性及运用,求出函数在定义域上的解析式是解题的关键,考查解决恒成立问题的常用方法:参数分离,必须掌握.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
某科室派出4名调研员到3个学校,调研高三复习备考近况,要求每个学校至少一名,则不同的分配方案的种数是( )
| A、144 | B、72 | C、36 | D、48 |
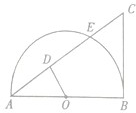 如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D.
如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D. (文)定义区间(c,d),[c,d),(c,d],[c,d]的长度均为d-c,其中d>c.
(文)定义区间(c,d),[c,d),(c,d],[c,d]的长度均为d-c,其中d>c.