题目内容
已知f(x)=x3+ax2+bx+c在x=1,x=-
时,都取得极值.
(1)求a、b的值;
(2)若对x∈[-1,2],有f(x)<
恒成立,求c的取值范围.
| 2 |
| 3 |
(1)求a、b的值;
(2)若对x∈[-1,2],有f(x)<
| 1 |
| c |
考点:利用导数研究函数的极值
专题:函数的性质及应用,导数的概念及应用
分析:(1)根据极值点处的导数为零,列出关于a,b的方程组求解;
(2)只需f(x)在[-1,2]上的最大值小于c即可,结合导数求出f(x)在该区间上的最大值,构造关于c的不等式.
(2)只需f(x)在[-1,2]上的最大值小于c即可,结合导数求出f(x)在该区间上的最大值,构造关于c的不等式.
解答:
解(1)由已知得f′(x)=3x2+2ax+b,因为x=1,x=-
是极值点,
所以
,即
,解得a=-
,b=-2.
(2)由(1)得f(x)=x3-
x2-2x+c,
所以f′(x)=3x2-x-2=3(x+
)(x-1).令f′(x)=0得x=-
或x=1.
结合可导函数在闭区间上最值的求法可知,函数的最值必在区间内导数为0或端点处取得.
因为f(-1)=c+
,f(-
)=c+
,f(1)=c-
,f(2)=c+2.
可见最大值为f(2)=c+2.由题意得c+2<
.即
<0,
即
或
.
解得c<-1-
或0<c<
-1.
故c的范围是c<-1-
或0<c<
-1.
| 2 |
| 3 |
所以
|
|
| 1 |
| 2 |
(2)由(1)得f(x)=x3-
| 1 |
| 2 |
所以f′(x)=3x2-x-2=3(x+
| 2 |
| 3 |
| 2 |
| 3 |
结合可导函数在闭区间上最值的求法可知,函数的最值必在区间内导数为0或端点处取得.
因为f(-1)=c+
| 1 |
| 2 |
| 2 |
| 3 |
| 22 |
| 27 |
| 3 |
| 2 |
可见最大值为f(2)=c+2.由题意得c+2<
| 1 |
| c |
| c2+2c-1 |
| c |
即
|
|
解得c<-1-
| 2 |
| 2 |
故c的范围是c<-1-
| 2 |
| 2 |
点评:本题考查了导数求极值的基本思路,以及利用利用导数研究函数的单调性求最值,解决不等式恒成立问题的思路.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
在锐角△ABC中,则有( )
| A、cosA>sinB且cosB>sinA |
| B、cosA<sinB且cosB<sinA |
| C、cosA>sinB且cosB<sinA |
| D、cosA<sinB且cosB>sinA |
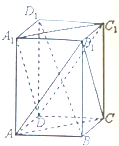 如图,在长方体ABCD-A1B1C1D1中,BB1=BC.
如图,在长方体ABCD-A1B1C1D1中,BB1=BC.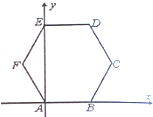 如图,正六边形ABCDEF的边长为2,分别以AB,AE所在直线为x,y轴建立直角边坐标系,用斜二测画法得到水平放置的正六边形ABCDEF的直观图A′B′C′D′E′F′,则六边形A′B′C′D′E′F′的面积为
如图,正六边形ABCDEF的边长为2,分别以AB,AE所在直线为x,y轴建立直角边坐标系,用斜二测画法得到水平放置的正六边形ABCDEF的直观图A′B′C′D′E′F′,则六边形A′B′C′D′E′F′的面积为