题目内容
如图，在△ABC中，∠ABC=60°，∠BAC=90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC=90°．
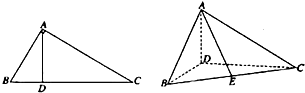
（Ⅰ）若BD=1，求三棱锥A-BCD的体积；
（Ⅱ）证明：平面ADB⊥平面BDC；
（Ⅲ）设E为BC的中点，求AE与DB所成的角的余弦值．
（Ⅰ）若BD=1，求三棱锥A-BCD的体积；
（Ⅱ）证明：平面ADB⊥平面BDC；
（Ⅲ）设E为BC的中点，求AE与DB所成的角的余弦值．
考点：平面与平面垂直的判定,棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题：证明题,空间位置关系与距离
分析：（1）根据几何体的体积公式，结合几何体的性质求解，
（2）运用判断定理证明，找线线位置关系．
（3）运用向量的坐标，结合向量的数量积与夹角的关系求解．
（2）运用判断定理证明，找线线位置关系．
（3）运用向量的坐标，结合向量的数量积与夹角的关系求解．
解答：
解（Ⅰ）BD=1，
根据图形可得：AD=
，AB=2，BC=4，DC=3
∴三棱锥A-BCD的体积为
×
×1×3×
=
，
∴得体积为
，
（Ⅱ）∵折起前AD是BC边上的高，
∴当△ABD折起后，AD⊥DC，AD⊥DB，
又DB∩DC=D，
∴AD⊥平面BDC，
∵AD?平面BDC．
∴平面ABD⊥平面BDC，
（Ⅲ）由∠BDC=90°及（Ⅰ）知DA，DB，DC两两垂直，
不妨设|BD|=1，
以D为坐标原点，以
，
，
所在直线x，y，z轴建立如图所示的空间直角坐标系，
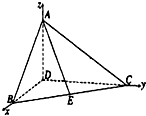
易得D（0，0，0），B（1，0，0），C（0，3，0），A（0，0，
），E（
，
，0），
∴
=（
，
，-
），
=（1，0，0，），
∴
与
夹角的余弦值为
=
=
，
故AE与DB所成的角的余弦值
根据图形可得：AD=
| 3 |
∴三棱锥A-BCD的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴得体积为
| ||
| 2 |
（Ⅱ）∵折起前AD是BC边上的高，
∴当△ABD折起后，AD⊥DC，AD⊥DB，
又DB∩DC=D，
∴AD⊥平面BDC，
∵AD?平面BDC．
∴平面ABD⊥平面BDC，
（Ⅲ）由∠BDC=90°及（Ⅰ）知DA，DB，DC两两垂直，
不妨设|BD|=1，
以D为坐标原点，以
| DB |
| DC |
| DA |
易得D（0，0，0），B（1，0，0），C（0，3，0），A（0，0，
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| AE |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| BD |
∴
| AE |
| DB |
| ||||
|
|
| ||||
1×
|
| ||
| 22 |
故AE与DB所成的角的余弦值
| ||
| 22 |
点评：本题考查了立体几何，空间向量与坐标系的关系，运用向量的知识判断垂直，求夹角；属于难题．
练习册系列答案
相关题目
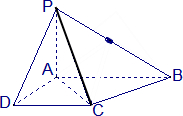已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=
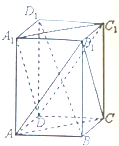如图，在长方体ABCD-A1B1C1D1中，BB1=BC．
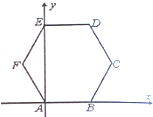如图，正六边形ABCDEF的边长为2，分别以AB，AE所在直线为x，y轴建立直角边坐标系，用斜二测画法得到水平放置的正六边形ABCDEF的直观图A′B′C′D′E′F′，则六边形A′B′C′D′E′F′的面积为