题目内容
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设 H1(X)=max{f(x),g(x)},max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值,记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A、a2-2a-16 |
| B、a2+2a-16 |
| C、16 |
| D、-16 |
考点:二次函数的性质
专题:函数的性质及应用
分析:本选择题宜采用特殊值法.取a=-2,则f(x)=x2+4,g(x)=-x2-8x+4.画出它们的图象,如图所示.从而得出H1(x)的最小值为两图象右边交点的纵坐标,H2(x)的最大值为两图象左边交点的纵坐标,再将两函数图象对应的方程组成方程组,求解即得.
解答:
解:取a=-2,则f(x)=x2+4,g(x)=-x2-8x+4.画出它们的图象,如图所示.
则H1(x)的最小值为两图象右边交点的纵坐标,H2(x)的最大值为两图象左边交点的纵坐标,
由
解得
或
,
∴A=4,B=20,A-B=-16.
故选D.

则H1(x)的最小值为两图象右边交点的纵坐标,H2(x)的最大值为两图象左边交点的纵坐标,
由
|
解得
|
|
∴A=4,B=20,A-B=-16.
故选D.
点评:本题主要考查了二次函数的图象与性质、函数最值的应用等,考查了数形结合的思想,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
设b=log32,a=ln2,c=0.5-0.01,则( )
| A、b<c<a |
| B、b<a<c |
| C、c<a<b |
| D、c<b<a |
若函数y=
x3-x2+1(0<x<2)的图象上任意点处切线的倾斜角为α,则α的最小值是( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在锐角△ABC中,则有( )
| A、cosA>sinB且cosB>sinA |
| B、cosA<sinB且cosB<sinA |
| C、cosA>sinB且cosB<sinA |
| D、cosA<sinB且cosB>sinA |
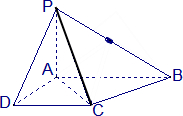 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=