题目内容
 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE和CF的中点.(1)求证:AF∥平面BDGH:
(2)求VE-BFH.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)设AC∩BD=O,连接OH,证明OH∥AF,即可证明AF∥平面BDGH;
(2)由面面垂直的性质可证AC与平面BDEF垂直,可得H到平面BDEF的距离为CO的一半,再利用等体积转换,即可得出结论.
(2)由面面垂直的性质可证AC与平面BDEF垂直,可得H到平面BDEF的距离为CO的一半,再利用等体积转换,即可得出结论.
解答:
(1)证明:设AC∩BD=O,连接OH,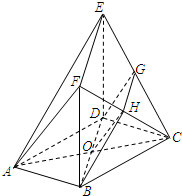
在△ACF中,因为OA=OC,CH=HF,
所以OH∥AF,
又因为OH?平面BDGH,AF?平面BDGH,
所以OH∥平面BDGH.…(6分)
(2)解:因为四边形是正方形,
所以AC⊥BD.
又因为平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,
且AC?平面ABCD,
所以AC⊥平面BDEF…(8分)
则H到平面BDEF的距离为CO的一半
又因为AO=
,三角形BEF的面积
×3×2
=3
,
所以VE-BFH=VH-BEF=
×3
×
=1…(12分)

在△ACF中,因为OA=OC,CH=HF,
所以OH∥AF,
又因为OH?平面BDGH,AF?平面BDGH,
所以OH∥平面BDGH.…(6分)
(2)解:因为四边形是正方形,
所以AC⊥BD.
又因为平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,
且AC?平面ABCD,
所以AC⊥平面BDEF…(8分)
则H到平面BDEF的距离为CO的一半
又因为AO=
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
所以VE-BFH=VH-BEF=
| 1 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查了面面垂直的性质,面面平行的判定,考查了求三棱锥的体积,考查了学生的空间想象能力与推理论证能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目