题目内容
已知函数y=
cos4x+sin4x,求函数的最小正周期,递增区间及最大值.
| 3 |
考点:两角和与差的正弦函数,正弦函数的图象
专题:三角函数的图像与性质
分析:利用两角和公式对函数解析式化简,利用周期公式求得函数最小正周期,根据正弦函数图象与性质求得函数的最大值和单调增区间.
解答:
解:y=2(
cos4x+
sin4x)=2sin(4x+
),
∴T=
=
,
ymax=2,
由2kπ-
≤4x+
≤2kπ+
,得
-
≤x≤
+
,k∈Z,
即函数的单调增区间为[
-
,
+
](k∈Z).
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴T=
| 2π |
| 4 |
| π |
| 2 |
ymax=2,
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 24 |
| kπ |
| 2 |
| π |
| 24 |
即函数的单调增区间为[
| kπ |
| 2 |
| 5π |
| 24 |
| kπ |
| 2 |
| π |
| 24 |
点评:本题主要考查了两角和与差的正弦函数,三角函数图象与性质.考查了学生对三角函数基础知识的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE和CF的中点.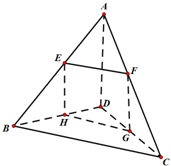 空间四边形ABCD中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于E,F,H.
空间四边形ABCD中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于E,F,H. 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=