题目内容
已知函数f(x)=x3+(a-1)x2+bx,f(x)在x=1处的切线斜率为-9,且f(x)的导函数f′(x)为偶函数.
(Ⅰ)求a,b的值;
(Ⅱ) 求f(x)的极值.
(Ⅰ)求a,b的值;
(Ⅱ) 求f(x)的极值.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:综合题,导数的概念及应用
分析:(Ⅰ)先利用导数求出在x=1处的导函数值,再利用f(x)的导函数f′(x)为偶函数,建立方程,即可求a,b的值;
(Ⅱ)确定函数的单调性,即可求f(x)的极值.
(Ⅱ)确定函数的单调性,即可求f(x)的极值.
解答:
解:(Ⅰ)依题意得f′(x)=3x2+2(a-1)x+b,
∵函数f(x)=x3+(a-1)x2+bx,f(x)在x=1处的切线斜率为-9,且f(x)的导函数f′(x)为偶函数,
∴
,
∴a=1,b=-12;
(Ⅱ)由(Ⅰ)知f′(x)=3x2-12=0,可得x=±2,
x∈(-∞,-2),函数单调递增,x∈(-2,2),函数单调递减,x∈(2,+∞),函数单调递增,
∴x=-2时,函数取得极大值16,x=2时,函数取得极小值-16.
∵函数f(x)=x3+(a-1)x2+bx,f(x)在x=1处的切线斜率为-9,且f(x)的导函数f′(x)为偶函数,
∴
|
∴a=1,b=-12;
(Ⅱ)由(Ⅰ)知f′(x)=3x2-12=0,可得x=±2,
x∈(-∞,-2),函数单调递增,x∈(-2,2),函数单调递减,x∈(2,+∞),函数单调递增,
∴x=-2时,函数取得极大值16,x=2时,函数取得极小值-16.
点评:本小题主要考查导数的几何意义、利用导数研究曲线上某点切线方程、考查函数的极值等基础知识,考查运算求解能力.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE和CF的中点.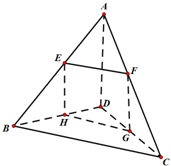 空间四边形ABCD中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于E,F,H.
空间四边形ABCD中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于E,F,H. 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=