题目内容
3.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )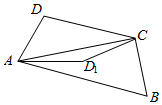
| A. | 椭圆的一段 | B. | 抛物线的一段 | C. | 一段圆弧 | D. | 双曲线的一段 |
分析 过B作AC的垂线BE,过D作AC的垂线DF,连接DE,BF,然后证明在翻折过程中,BD中点到BE的中点的距离为定值得答案.
解答 解:如图,过B作AC的垂线BE,过D作AC的垂线DF,连接DE,BF,
取BE中点为O,则在△BDE中,OM为△BDE的中位线,则OM=$\frac{1}{2}DE$,
当△ADC沿着AC翻折到ADlC时,△DEF翻折到△D1EF,在△BD1E中,OM1为△BD1E的中位线,则$O{M}_{1}=\frac{1}{2}{D}_{1}E$,
而翻折过程中,DE=D1E,∴OM=OM1,
∴翻折过程中线段DB中点M的轨迹是以O为圆心,以$\frac{1}{2}DE$为半径的一段圆弧.
故选:C.
点评 本题考查轨迹方程,考查了学生的空间想象能力和思维能力,有一定难度.

练习册系列答案
相关题目
14.如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2AD,则异面直线A1B与AD1所成角的余弦值为( )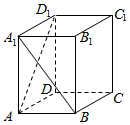

| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
8.已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(1),则f′(1)的值等于( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |