题目内容
13.若函数f(x)=x•|2x-a|(a>0)在区间[1,2]上的最小值为2,则a=5.分析 由a>0,结合y=f(x)的图象可得f(x)在[1,2]的最小值可以是f(1),或f(2),f($\frac{a}{2}$).分别计算求得a,将绝对值去掉,运用二次函数的对称轴和区间的关系,结合单调性,即可判断a的值.
解答 解:由a>0,结合y=f(x)的图象可得f(x)在[1,2]的最小值
可以是f(1),或f(2),f($\frac{a}{2}$).
由f($\frac{a}{2}$)=0,不成立;
由f(1)=|2-a|=2,解得a=0(舍去)或a=4,
当a=4时,f(x)=x|2x-4|在[1,2],即有:f(x)=2x(2-x)在[1,2]递减,
可得f(1)取得最大值,且为2;
由f(2)=2|4-a|=2,解得a=3或a=5.
当a=3时,f(x)=x|2x-3|在[1,2]即为:f(x)=$\left\{\begin{array}{l}{3x-2{x}^{2},1≤x≤1.5}\\{2{x}^{2}-3x,1.5<x≤2}\end{array}\right.$,
可得f(x)在[1,1.5]递减,在[1.5,2]递增,
即有f(1.5)=0为最小值,故a=3不成立;
当a=5时,f(x)=x|2x-5|在[1,2]即为:f(x)=x(5-2x),
可得f(x)在[1,$\frac{5}{4}$]递增,在[$\frac{5}{4}$,2]递减,
即有f(2)取得最小值,且为2,成立.
综上可得a=4或5.
故答案为:5.
点评 本题考查函数的最值的求法,注意运用分类讨论的思想方法,考查二次函数的最值的求法,注意讨论对称轴和区间的关系,属于中档题.

练习册系列答案
相关题目
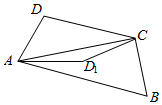
3.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )

| A. | 椭圆的一段 | B. | 抛物线的一段 | C. | 一段圆弧 | D. | 双曲线的一段 |
18.设定义在(0,+∞)上的单调函数f(x)对任意的x∈(0,+∞)都有f(f(x)-log2x)=6,则不等式f(x)>3的解集为( )
| A. | {x|x>1} | B. | {x|x>$\frac{1}{2}$} | C. | {x|0<x<1} | D. | {x|0<x<2} |