题目内容
14.如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2AD,则异面直线A1B与AD1所成角的余弦值为( )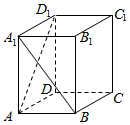
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1B与AD1所成角的余弦值.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设AA1=2AB=2AD=2,
则A1(1,0,2),B(1,1,0),A(1,0,0),D1(0,0,2),
$\overrightarrow{{A}_{1}B}$=(0,1,-2),$\overrightarrow{A{D}_{1}}$=(-1,0,2),
设异面直线A1B与AD1所成角为θ,
则cosθ=$\frac{|\overrightarrow{{A}_{1}B}•\overrightarrow{A{D}_{1}}|}{|\overrightarrow{{A}_{1}B}|•|\overrightarrow{A{D}_{1}}|}$=$\frac{4}{\sqrt{5}•\sqrt{5}}$=$\frac{4}{5}$.
∴异面直线A1B与AD1所成角的余弦值为$\frac{4}{5}$.
故选:D.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
4.动点P到两定点F1(0,-4),F2(0,4)的距离之和为10,则动点P的轨迹方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{25}=1$ | C. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{100}+\frac{y^2}{36}=1$ |
5.与圆x2+y2+8x+15=0及圆x2+y2-8x+12=0都外切的圆的圆心在( )
| A. | 一个椭圆上 | B. | 一条抛物线上 | C. | 双曲线的一支上 | D. | 一个圆上 |
2.将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,则a的最大值为( )
| A. | $\frac{{2\sqrt{2}-\sqrt{6}}}{6}$ | B. | $\frac{{2\sqrt{3}-\sqrt{6}}}{6}$ | C. | $\frac{{2\sqrt{3}-2\sqrt{2}}}{3}$ | D. | $\frac{{3\sqrt{2}-2\sqrt{3}}}{3}$ |
9.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在这30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.能否在犯错误的概率不超过0.005的前提下认为肥胖与常喝碳酸饮料有关?说明你的理由.
(2)现从常喝碳酸饮料的学生中抽取3人参加电视节目,记ξ表示常喝碳酸饮料且肥胖的学生人数,求ξ的分布列及数学期望.
参考数据:
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(2)现从常喝碳酸饮料的学生中抽取3人参加电视节目,记ξ表示常喝碳酸饮料且肥胖的学生人数,求ξ的分布列及数学期望.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.某学校为挑选参加地区汉字听写大赛的学生代表,从全校报名的1200人中筛选出300人参加听写比赛,然后按听写比赛成绩择优选取75人再参加诵读比赛.
(1)从参加听写比赛的学生中随机抽取了24名学生的比赛成绩整理成表:
请你根据该样本数据估计进入诵读比赛的分数线大约是多少?
(2)若学校决定,从诵读比赛的女生的前4名a,b,c,d和男生的前两名e,f中挑选两名学生作为代表队队长,请你求出队长恰好为一男一女的概率.
(1)从参加听写比赛的学生中随机抽取了24名学生的比赛成绩整理成表:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95] |
| 1 | 2 | 6 | 9 | 4 | 1 | 1 |
(2)若学校决定,从诵读比赛的女生的前4名a,b,c,d和男生的前两名e,f中挑选两名学生作为代表队队长,请你求出队长恰好为一男一女的概率.
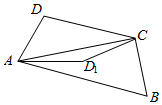
3.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )

| A. | 椭圆的一段 | B. | 抛物线的一段 | C. | 一段圆弧 | D. | 双曲线的一段 |