题目内容
11.已知$sinα=-\frac{4}{5}$,α在第三象限,求cosα,tanα的值.分析 由sinα的值及α为第三象限角,利用同角三角函数间的基本关系求出cosα的值,进而求出tanα的值即可.
解答 解:∵sinα=-$\frac{4}{5}$,α在第三象限,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{3}{5}$,tanα=$\frac{sinα}{cosα}$=$\frac{-\frac{4}{5}}{-\frac{3}{5}}$=$\frac{4}{3}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
2.将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,则a的最大值为( )
| A. | $\frac{{2\sqrt{2}-\sqrt{6}}}{6}$ | B. | $\frac{{2\sqrt{3}-\sqrt{6}}}{6}$ | C. | $\frac{{2\sqrt{3}-2\sqrt{2}}}{3}$ | D. | $\frac{{3\sqrt{2}-2\sqrt{3}}}{3}$ |
19.某学校为挑选参加地区汉字听写大赛的学生代表,从全校报名的1200人中筛选出300人参加听写比赛,然后按听写比赛成绩择优选取75人再参加诵读比赛.
(1)从参加听写比赛的学生中随机抽取了24名学生的比赛成绩整理成表:
请你根据该样本数据估计进入诵读比赛的分数线大约是多少?
(2)若学校决定,从诵读比赛的女生的前4名a,b,c,d和男生的前两名e,f中挑选两名学生作为代表队队长,请你求出队长恰好为一男一女的概率.
(1)从参加听写比赛的学生中随机抽取了24名学生的比赛成绩整理成表:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95] |
| 1 | 2 | 6 | 9 | 4 | 1 | 1 |
(2)若学校决定,从诵读比赛的女生的前4名a,b,c,d和男生的前两名e,f中挑选两名学生作为代表队队长,请你求出队长恰好为一男一女的概率.
3.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )
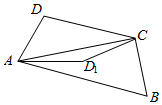

| A. | 椭圆的一段 | B. | 抛物线的一段 | C. | 一段圆弧 | D. | 双曲线的一段 |
20.曲线y=-$\frac{1}{2}$x+lnx的切线是直线y=$\frac{1}{2}$x+b,则b的值为( )
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 1 |