题目内容
18.已知定圆A:x2+y2-4x=0,定直线L:x+1=0,求与定圆A外切又与定直线L相切的圆的圆心轨迹方程.分析 化圆的一般式方程为标准方程,利用直线与圆、圆与圆位置关系列等式得答案.
解答 解:由圆A:x2+y2-4x=0,得(x-2)2+y2=4,
如图
设M(x,y),由题意可得:
x-(-1)=|MA|-2,
即x+1=$\sqrt{(x-2)^{2}+{y}^{2}}$-2,整理得:y2=12x+5.
∴动圆的圆心轨迹为y2=12x+5.
点评 本题考查轨迹方程的求法,考查直线与圆、圆与圆位置关系的应用,是中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在这30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.能否在犯错误的概率不超过0.005的前提下认为肥胖与常喝碳酸饮料有关?说明你的理由.
(2)现从常喝碳酸饮料的学生中抽取3人参加电视节目,记ξ表示常喝碳酸饮料且肥胖的学生人数,求ξ的分布列及数学期望.
参考数据:
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(2)现从常喝碳酸饮料的学生中抽取3人参加电视节目,记ξ表示常喝碳酸饮料且肥胖的学生人数,求ξ的分布列及数学期望.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )
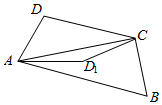

| A. | 椭圆的一段 | B. | 抛物线的一段 | C. | 一段圆弧 | D. | 双曲线的一段 |
7.期中考试后,我校对甲、乙两个文科班的数学考试成绩进行分析.规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的2×2列联表:
(1)求出表格中x,y的值;
(2)根据列联表的数据,判断是否有99%的把握认为“成绩与班级有关系”,并说明理由.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | 10 | x | 50 |
| 乙班 | y | 30 | 50 |
| 合计 | 30 | 70 | 100 |
(2)根据列联表的数据,判断是否有99%的把握认为“成绩与班级有关系”,并说明理由.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |