题目内容
12.已知函数$f(x)=\left\{\begin{array}{l}2,x>m\\{x^2}+4x+2,x≤m\end{array}\right.$的图象与直线y=x恰有三个公共点,则实数m的取值范围是[-1,2).分析 由题意可得只要满足直线y=x和射线y=2(x>m)有一个交点,而且直线y=x与函数f(x)=x2+4x+2的两个交点即可,画图便知,直线y=x与函数f(x)=x2+4x+2的图象的两个交点为(-2,-2)(-1,-1),由此可得实数m的取值范围.
解答 解:由题意可得射线y=x与函数f(x)=2(x>m)有且只有一个交点.
而直线y=x与函数f(x)=x2+4x+2,至多两个交点,
题目需要三个交点,则只要满足直线y=x与函数f(x)=x2+4x+2的图象有两个交点即可,
画图便知,y=x与函数f(x)=x2+4x+2的图象交点为A(-2,-2)、B(-1,-1),故有 m≥-1.
而当m≥2时,直线y=x和射线y=2(x>m)无交点,故实数m的取值范围是[-1,2),
故答案为:[-1,2)
点评 本题考查的知识点分段函数,分类讨论思想,数形结合思想,难度中档.

练习册系列答案
相关题目
2.将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,则a的最大值为( )
| A. | $\frac{{2\sqrt{2}-\sqrt{6}}}{6}$ | B. | $\frac{{2\sqrt{3}-\sqrt{6}}}{6}$ | C. | $\frac{{2\sqrt{3}-2\sqrt{2}}}{3}$ | D. | $\frac{{3\sqrt{2}-2\sqrt{3}}}{3}$ |
3.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )
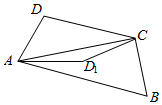

| A. | 椭圆的一段 | B. | 抛物线的一段 | C. | 一段圆弧 | D. | 双曲线的一段 |
20.曲线y=-$\frac{1}{2}$x+lnx的切线是直线y=$\frac{1}{2}$x+b,则b的值为( )
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 1 |
7.期中考试后,我校对甲、乙两个文科班的数学考试成绩进行分析.规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的2×2列联表:
(1)求出表格中x,y的值;
(2)根据列联表的数据,判断是否有99%的把握认为“成绩与班级有关系”,并说明理由.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | 10 | x | 50 |
| 乙班 | y | 30 | 50 |
| 合计 | 30 | 70 | 100 |
(2)根据列联表的数据,判断是否有99%的把握认为“成绩与班级有关系”,并说明理由.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |