题目内容
已知奇函数f(x)在x≥0时的图象如图所示,则不等式f(x)<0的解集为( )


| A、(-1,0)∪(1,2) |
| B、(-∞,2)∪(-1,0)∪(1,2) |
| C、(-2,-1)∪(1,2) |
| D、(-1,0)∪(0,1) |
考点:函数的图象
专题:函数的性质及应用
分析:由f(x)是奇函数得函数图象关于原点对称,可画出y轴左侧的图象,利用两因式异号相乘得负,得出f(x)的正负,由图象可求出x的范围得结果.
解答:
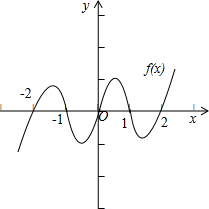 解:由题意可得,函数f(x)的图象关于原点对称,可得函数在R上的图象,如图:
解:由题意可得,函数f(x)的图象关于原点对称,可得函数在R上的图象,如图:
由图象可知,不等式f(x)<0,不等式的解集为(-∞,2)∪(-1,0)∪(1,2)
故选B.
 解:由题意可得,函数f(x)的图象关于原点对称,可得函数在R上的图象,如图:
解:由题意可得,函数f(x)的图象关于原点对称,可得函数在R上的图象,如图:由图象可知,不等式f(x)<0,不等式的解集为(-∞,2)∪(-1,0)∪(1,2)
故选B.
点评:由函数的奇偶性得出整个图象,分类讨论的思想得出函数值的正负,数形结合得出自变量的范围,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
函数y=-
的反函数的图象关于( )
| 2x-1 |
| x+3 |
| A、直线y=x对称 |
| B、点(3,2)对称 |
| C、点(-3,-2)对称 |
| D、点(-2,-3)对称 |
不等式|x+2|+|x-1|<4的解集为( )
| A、(-2,1) | ||||
| B、[-2,1] | ||||
C、(-∞,
| ||||
D、(-
|
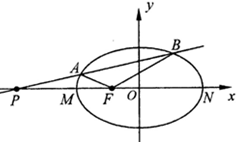 如图,点F是椭圆
如图,点F是椭圆