题目内容
不等式|x+2|+|x-1|<4的解集为( )
| A、(-2,1) | ||||
| B、[-2,1] | ||||
C、(-∞,
| ||||
D、(-
|
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由条件根据绝对值的几何意义,求得不等式|x+2|+|x-1|<4的解集.
解答:
解:|x+2|+|x-1|表示数轴上的x对应点到-2、1对应点的距离之和,
而数轴上-
、
对应点到-2、1对应点的距离之和正好等于4,
故不等式|x+2|+|x-1|<4的解集为(-
、
),
故选:D.
而数轴上-
| 5 |
| 2 |
| 3 |
| 2 |
故不等式|x+2|+|x-1|<4的解集为(-
| 5 |
| 2 |
| 3 |
| 2 |
故选:D.
点评:本题主要考查绝对值的意义,绝对值不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知奇函数f(x)在x≥0时的图象如图所示,则不等式f(x)<0的解集为( )


| A、(-1,0)∪(1,2) |
| B、(-∞,2)∪(-1,0)∪(1,2) |
| C、(-2,-1)∪(1,2) |
| D、(-1,0)∪(0,1) |
程序:输入2,3,则程序执行的结果为( )


| A、2,3 | B、3,2 |
| C、2,2 | D、3,3 |
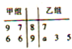 如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=