题目内容
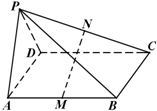 四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.
四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.(Ⅰ)证明:MN∥平面PAD.
(Ⅱ)若CM=PM,MN⊥AB,证明:平面PAD⊥平面PDC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
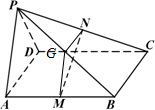
分析:(Ⅰ)作PB的中点G,连结NG,MG,由N,G,均为中点,推断出NG∥BC,进而根据BC∥AD,推断出NG∥AD,最后根据线面平行的判定定理推断出NG∥平面PAD,同理可知MG∥平面PAD,进而根据面面平行的判定定理推断出平面MNG∥平面PAD,根据面面平行的性质推断出MN∥平面PAD.
(Ⅱ)由CM=PM,N为中点,推断出MN⊥PC,进而根据AB∥CD,MN⊥AB,推断出MN⊥CD,利用线面垂直的判定定理可知MN⊥平面PDC,进而由MN∥平面PAD.推断出平面PAD⊥平面PDC.
(Ⅱ)由CM=PM,N为中点,推断出MN⊥PC,进而根据AB∥CD,MN⊥AB,推断出MN⊥CD,利用线面垂直的判定定理可知MN⊥平面PDC,进而由MN∥平面PAD.推断出平面PAD⊥平面PDC.
解答:
证明:(Ⅰ)作PB的中点G,连结NG,MG,
∵N,G,均为中点,
∴NG∥BC,
∵BC∥AD,
∴NG∥AD,
∵AD?平面PAD,NG?平面PAD,
∴NG∥平面PAD,
同理可知MG∥平面PAD,
∵MG?平面MNG,NG?平面MNG,MG∩NG=G,
∴平面MNG∥平面PAD,
∵MN?平面MNG,
∴MN∥平面PAD.
(Ⅱ)∵CM=PM,N为中点,
∴MN⊥PC,
∵AB∥CD,MN⊥AB,
∴MN⊥CD,
∵CD?平面PDC,PC?平面PDC,CD∩PC=C,
∴MN⊥平面PDC,
∵MN∥平面PAD.
∴平面PAD⊥平面PDC.
∵N,G,均为中点,
∴NG∥BC,
∵BC∥AD,
∴NG∥AD,
∵AD?平面PAD,NG?平面PAD,
∴NG∥平面PAD,
同理可知MG∥平面PAD,
∵MG?平面MNG,NG?平面MNG,MG∩NG=G,
∴平面MNG∥平面PAD,
∵MN?平面MNG,
∴MN∥平面PAD.
(Ⅱ)∵CM=PM,N为中点,
∴MN⊥PC,
∵AB∥CD,MN⊥AB,
∴MN⊥CD,
∵CD?平面PDC,PC?平面PDC,CD∩PC=C,
∴MN⊥平面PDC,
∵MN∥平面PAD.
∴平面PAD⊥平面PDC.

点评:本题主要考查了面面垂直的判定定理,线面平行的判定定理的运用.第一问中,先证明出面面平行是前提.

练习册系列答案
相关题目
下列说法中正确的个数有( )
(1)平行于同一直线的两个平面平行;
(2)平行于同一平面的两个平面平行;
(3)垂直于同一直线的两直线平行;
(4)垂直于同一平面的两直线平行;
(5)垂直于同一直线的两个平面平行.
(1)平行于同一直线的两个平面平行;
(2)平行于同一平面的两个平面平行;
(3)垂直于同一直线的两直线平行;
(4)垂直于同一平面的两直线平行;
(5)垂直于同一直线的两个平面平行.
| A、1 | B、2 | C、3 | D、4 |
设r>0,那么直线xcosθ+ysinθ=r(θ是常数)与圆
(φ是参数)的位置关系是( )
|
| A、相交 | B、相切 |
| C、相离 | D、视r的大小而定 |
“sinA=
”是“A=45°”的( )
| ||
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |