题目内容
已知双曲线x2-
=1的左右焦点分别为F1、F2，过F2的直线交该双曲线右支于两点A、B．若|AB|=8，则△ABF1的周长为（ ）
| y2 |
| 3 |
| A、4 | ||
| B、20 | ||
C、4
| ||
| D、8 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的定义和性质，即可求出三角形的周长．
解答：
解：由双曲线的方程可知a=1，
则|AF1|-|AF2|=2，|BF1|-|BF2|=2，
则|AF1|+|BF1|-（|BF2|+|AF2|）=4，
即|AF1|+|BF1|=|BF2|+|AF2|+4=|AB|+4=8+4=12，
则△ABF1的周长为|AF1|+|BF1|+|AB|=12+8=20，
故选：B
解：由双曲线的方程可知a=1，则|AF1|-|AF2|=2，|BF1|-|BF2|=2，
则|AF1|+|BF1|-（|BF2|+|AF2|）=4，
即|AF1|+|BF1|=|BF2|+|AF2|+4=|AB|+4=8+4=12，
则△ABF1的周长为|AF1|+|BF1|+|AB|=12+8=20，
故选：B
点评：本题主要考查双曲线的定义，根据双曲线的定义得到A，B到两焦点距离之差是个常数是解决本题的关键．
练习册系列答案
相关题目
若k∈R，则k=5是方程
-
=1表示双曲线的（ ）条件．
| x2 |
| k-3 |
| y2 |
| k+3 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
将正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，E是CD的中点，则AE与平面ABD所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）=
mx2+lnx-2x在定义域内是增函数，则实数m的取值范围为（ ）
| 1 |
| 2 |
| A、[0，+∞） |
| B、（0，+∞） |
| C、[-3，+∞） |
| D、[1，+∞） |
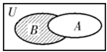已知全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，则图中阴影部分所表示的集合是（ ）| A、{1，2，4} |
| B、{3，7，8} |
| C、{1，2，4，6} |
| D、{3，6，7，8} |
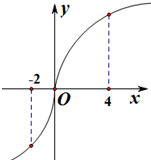已知定义在R上的函数f（x）满足f（4）=f（-2）=1，且y=f′（x）的图象如图所示，则不等式f（x）＜1的解集是（ ）| A、（-2，0） |
| B、（0，4） |
| C、（-2，4） |
| D、（-∞，-2）∪（4，+∞） |
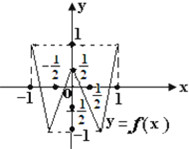已知函数y=f（x）的定义域和值域都是[-1，1]（其图象如图所示），函数g（x）=sinx，x∈[-π，π]．定义：当f（x1）=0（x1∈[-1，1]）且g（x2）=x1（x2∈[-π，π]）时，称x2是方程f（g（x））=0的一个实数根．则方程f（g（x））=0的所有不同实数根的个数是（ ）
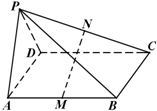四棱锥P-ABCD的底面ABCD是平行四边形，M、N分别是AB、PC的中点．