题目内容
下列说法中正确的个数有（ ）
（1）平行于同一直线的两个平面平行；
（2）平行于同一平面的两个平面平行；
（3）垂直于同一直线的两直线平行；
（4）垂直于同一平面的两直线平行；
（5）垂直于同一直线的两个平面平行．
（1）平行于同一直线的两个平面平行；
（2）平行于同一平面的两个平面平行；
（3）垂直于同一直线的两直线平行；
（4）垂直于同一平面的两直线平行；
（5）垂直于同一直线的两个平面平行．
| A、1 | B、2 | C、3 | D、4 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：分别根据面面平行，线面平行的性质进行判断即可得到结论．
解答：
解：（1）平行于同一直线的两个平面平行或者相交；故（1）错误，
（2）平行于同一平面的两个平面平行；正确，
（3）垂直于同一直线的两直线平行，相交或异面，故（3）错误，
（4）垂直于同一平面的两直线平行；正确，
（5）垂直于同一直线的两个平面平行．正确，
故正确的是（2）（4）（5），
故选：C
（2）平行于同一平面的两个平面平行；正确，
（3）垂直于同一直线的两直线平行，相交或异面，故（3）错误，
（4）垂直于同一平面的两直线平行；正确，
（5）垂直于同一直线的两个平面平行．正确，
故正确的是（2）（4）（5），
故选：C
点评：本题主要考查空间直线和平面平行或垂直的判断，要求熟练掌握相应的性质和判定定理．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
| ∫ | π 0 |
A、
| ||
B、
| ||
C、
| ||
| D、π2 |
若k∈R，则k=5是方程
-
=1表示双曲线的（ ）条件．
| x2 |
| k-3 |
| y2 |
| k+3 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
从分别写有1，2，3，4，5的五张卡片中任取两张，假设每张卡片被取到的概率相等，且每张卡片上只有一个数字，则收到的两张卡片上的数字之和为偶数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
过双曲线x2-y2=1的右焦点且与右支有两个交点的直线，其倾斜角范围是（ ）
| A、[0，π） | ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（0，
|
已知△ABC内一点P满足
=λ
+μ
，若△PAB的面积与△ABC的面积之比为1：3，△PAC的面积与△ABC的面积之比为1：4，则实数λ，μ的值为（ ）
| AP |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
将正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，E是CD的中点，则AE与平面ABD所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）=
mx2+lnx-2x在定义域内是增函数，则实数m的取值范围为（ ）
| 1 |
| 2 |
| A、[0，+∞） |
| B、（0，+∞） |
| C、[-3，+∞） |
| D、[1，+∞） |
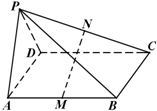四棱锥P-ABCD的底面ABCD是平行四边形，M、N分别是AB、PC的中点．