题目内容
设r>0,那么直线xcosθ+ysinθ=r(θ是常数)与圆
(φ是参数)的位置关系是( )
|
| A、相交 | B、相切 |
| C、相离 | D、视r的大小而定 |
考点:参数方程化成普通方程,直线与圆的位置关系
专题:坐标系和参数方程
分析:利用参数方程化为直角坐标方程,通过圆心与直线的距离与半径的关系,判断选项即可.
解答:
解:圆
的圆心为坐标原点,半径为r.
圆心到直线的距离为
=r,
所以直线与圆相切.
故选:B.
|
圆心到直线的距离为
| r | ||
|
所以直线与圆相切.
故选:B.
点评:本题考查点到直线的距离,直线与圆位置关系.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
从分别写有1,2,3,4,5的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则收到的两张卡片上的数字之和为偶数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为( )
| 1 |
| 2 |
| A、[0,+∞) |
| B、(0,+∞) |
| C、[-3,+∞) |
| D、[1,+∞) |
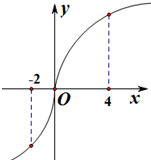 已知定义在R上的函数f(x)满足f(4)=f(-2)=1,且y=f′(x)的图象如图所示,则不等式f(x)<1的解集是( )
已知定义在R上的函数f(x)满足f(4)=f(-2)=1,且y=f′(x)的图象如图所示,则不等式f(x)<1的解集是( )| A、(-2,0) |
| B、(0,4) |
| C、(-2,4) |
| D、(-∞,-2)∪(4,+∞) |
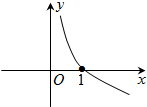 已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )
已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)<f(cosB) |
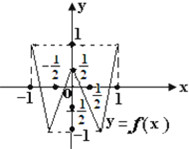 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )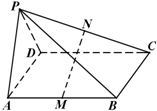 四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.
四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.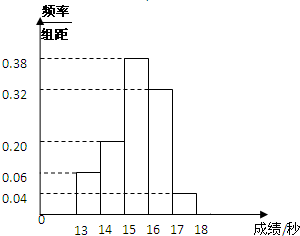 某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.
某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.