题目内容
以平面直角坐标系的原点为极点,以x轴的正半轴为极轴建立极坐标系.设曲线C的参数方程为
(α是参数),直线l的极坐标方程为ρcos(θ+
)=2
.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线l的距离的最大值.
|
| π |
| 6 |
| 3 |
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线l的距离的最大值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)利用极坐标和直角坐标的互化公式把直线l的极坐标方程化为直角坐标方程.利用同角三角函数的基本关系消去α,把曲线C的参数方程化为直角坐标方程.
(2)设点P(2cosα,
sinα),求得点P到直线l的距离d=
,tanβ=
,由此求得d的最大值.
(2)设点P(2cosα,
| 3 |
|
| ||||
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵直线l的极坐标方程为ρcos(θ+
)=2
,即ρ(
cosθ-
sinθ)=2
,
即
x-y-4
=0.
曲线C的参数方程为
(α是参数),利用同角三角函数的基本关系消去α,
可得
+
=1.
(2)设点P(2cosα,
sinα)为曲线C上任意一点,
则点P到直线l的距离d=
=
,tanβ=
,
故当cos(α+β)=-1时,d取得最大值为
.
| π |
| 6 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
即
| 3 |
| 3 |
曲线C的参数方程为
|
可得
| x2 |
| 4 |
| y2 |
| 3 |
(2)设点P(2cosα,
| 3 |
则点P到直线l的距离d=
|2
| ||||||
|
|
| ||||
| 2 |
| 1 |
| 2 |
故当cos(α+β)=-1时,d取得最大值为
| ||||
| 2 |
点评:本题主要考查把极坐标方程、参数方程化为直角坐标方程的方法,点到直线的距离公式、辅助角公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD的中点,则AE与平面ABD所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
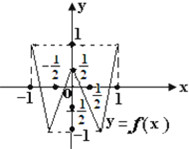 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )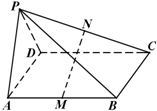 四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.
四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.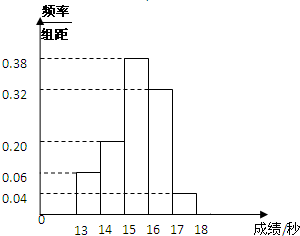 某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.
某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.