题目内容
已知矩阵M=
.
(Ⅰ)求M2,M3,并猜想Mn的表达式;
(Ⅱ)试求曲线x2+y2=1在矩阵M-1变换下所得曲线的方程.
|
(Ⅰ)求M2,M3,并猜想Mn的表达式;
(Ⅱ)试求曲线x2+y2=1在矩阵M-1变换下所得曲线的方程.
考点:几种特殊的矩阵变换
专题:选作题,矩阵和变换
分析:(Ⅰ)利用二阶矩阵的乘法,可求M2,M3,并猜想Mn的表达式;
(Ⅱ)先求出矩阵M-1,根据矩阵变换特点,写出两对坐标之间的关系,代入曲线x2+y2=1得到曲线x2+y2=1在矩阵M-1变换下所得曲线的方程.
(Ⅱ)先求出矩阵M-1,根据矩阵变换特点,写出两对坐标之间的关系,代入曲线x2+y2=1得到曲线x2+y2=1在矩阵M-1变换下所得曲线的方程.
解答:
解:(Ⅰ) M2=
=
,
M3=M2M=
=
猜想Mn=
…(3分)
(Ⅱ)∵|M|=
,∴M-1=
,
即在矩阵M-1的变换下有
,故
由x2+y2=1得x′2+(
y′)2=1,即x′2+
=1
故曲线x2+y2=1在矩阵M-1变换下所得曲线的方程为x2+
=1.…(7分)
|
|
|
M3=M2M=
|
|
|
猜想Mn=
|
(Ⅱ)∵|M|=
| 1 |
| 2 |
|
即在矩阵M-1的变换下有
|
|
由x2+y2=1得x′2+(
| 1 |
| 2 |
| y′2 |
| 4 |
故曲线x2+y2=1在矩阵M-1变换下所得曲线的方程为x2+
| y2 |
| 4 |
点评:本题主要考查二阶矩阵的变换,考查运算求解能力,比较基础.

练习册系列答案
相关题目
已知函数f(x)=
mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为( )
| 1 |
| 2 |
| A、[0,+∞) |
| B、(0,+∞) |
| C、[-3,+∞) |
| D、[1,+∞) |
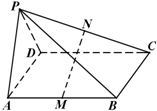 四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.
四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.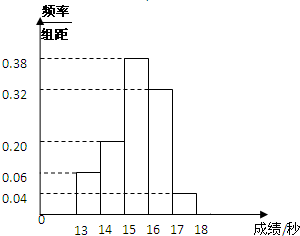 某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.
某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.