题目内容
已知直线l的参数方程为
(t为参数).以直角坐标系的原点为极点,x轴正半轴为极轴的圆C的极坐标方程为ρ=2cosθ.
(1)请将直线l转化为极坐标方程;
(2)若直线l与圆C交于A,B两点,点M(1,5),求|MA|•|MB|的值.
|
(1)请将直线l转化为极坐标方程;
(2)若直线l与圆C交于A,B两点,点M(1,5),求|MA|•|MB|的值.
考点:参数方程化成普通方程,平面直角坐标系与曲线方程,简单曲线的极坐标方程,参数的意义,直线的参数方程
专题:坐标系和参数方程
分析:(1)先将
(t为参数)消去参数t,得到普通方程,然后求解原点到直线的距离,求出极坐标方程;(2)求出圆的普通方程,代入直线的参数方程,利用参数方程分几何意义,直接求解|MA|•|MB|的值.
|
解答:
 解:(1)直线l的参数方程为
解:(1)直线l的参数方程为
(t为参数),化为直角坐标方程为:
x+y-5-
=0,
原点到直线的距离为:d=
=
.如图:
直线的极坐标方程是ρcos(θ-
)=
.
(2)由曲线C的极坐标方程是ρ=2cosθ化为直角坐标方程为:
x2+y2-2x=0,代入直线参数方程,可得(1+
t)2+(5-
t)2-2(1+
t)=0,
化简可得:t2-5
t+24=0.t1•t2=24.
∴|MA|•|MB|=24.
 解:(1)直线l的参数方程为
解:(1)直线l的参数方程为
|
| 3 |
| 3 |
原点到直线的距离为:d=
|5+
| ||||
|
5+
| ||
| 2 |
直线的极坐标方程是ρcos(θ-
| π |
| 6 |
5+
| ||
| 2 |
(2)由曲线C的极坐标方程是ρ=2cosθ化为直角坐标方程为:
x2+y2-2x=0,代入直线参数方程,可得(1+
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
化简可得:t2-5
| 3 |
∴|MA|•|MB|=24.
点评:本小题主要考查简单曲线的极坐标方程、直线的参数方程、直线与圆相交的性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.极坐标方程化成直角坐标方程关键是利用直角坐标与极坐标间的关系:ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.属于基础题.

练习册系列答案
相关题目
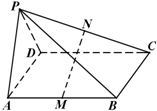 四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.
四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点.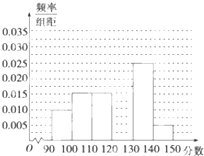 某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: